【题目】如图,对称轴为x=1的抛物线经过A(﹣1,0),B(4,5)两点.
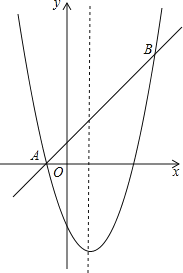
(1)求抛物线的解析式;
(2)P为直线AB上的动点,过点P作x轴的垂线交抛物线于点Q.
①当PQ=6时,求点P的坐标;
②是否存在点P,使以A、P、Q为顶点的三角形为等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)y=x2﹣2x﹣3;(2)①当PQ=6时,点P的坐标(1,2),(2,3),(﹣2,﹣1),(5,6);②存在点P,使以A、P、Q为顶点的三角形为等腰三角形,点P的坐标为P(4+![]() ,5+
,5+![]() )或(4﹣
)或(4﹣![]() ,5﹣
,5﹣![]() )或(4,5)或(3.4).
)或(4,5)或(3.4).
【解析】
试题分析:(1)根据题意确定抛物线与x轴的另一个交点,然后根据待定系数法即可求得;
(2)①先求得直线AB的解析式,设P(m,m+1),Q(m,m2﹣2m﹣3),则PQ=|m+1﹣m2+2m+3|=6,然后分m2﹣3m﹣4=﹣6或m2﹣3m﹣4=6两种情况求得m的值,从而求得P点的坐标;
②由勾股定理,得PA2=(m+1)2+(m+1)2;PQ2=[m+1﹣(m2﹣2m﹣3)]2,AQ2=(m+1)2+(m2﹣2m﹣3)2.然后分PA=PQ、PA=AQ、AQ=AP三种情况列出关于m的方程,解方程求得m的值,即可求得P点的坐标.
解:(1)对称轴为x=1的抛物线经过A(﹣1,0),得C(3,0),
设抛物线的解析式为y=ax2+bx+c,将A、B、C点坐标代入,得
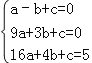 ,
,
解得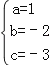 ,
,
设抛物线的解析式为y=x2﹣2x﹣3;
(2)①直线AB的解析式为y=x+1,设P(m,m+1),Q(m,m2﹣2m﹣3),
PQ=|m+1﹣m2+2m+3|=6,
当m2﹣3m﹣4=﹣6,
解得m=1,m=2,
∴P(1,2)或(2,3);
当m2﹣3m﹣4=6,解得m=﹣2,m=5,
∴P(﹣2,﹣1)或(5,6);
综上所述:当PQ=6时,点P的坐标(1,2),(2,3),(﹣2,﹣1),(5,6);
(3)∵A(﹣1,0),P(m,m+1),Q(m,m2﹣2m﹣3),由勾股定理,得
PA2=(m+1)2+(m+1)2;PQ2=[m+1﹣(m2﹣2m﹣3)]2,AQ2=(m+1)2+(m2﹣2m﹣3)2.
①当PA=PQ时,(m+1)2+(m+1)2=[m+1﹣(m2﹣2m﹣3)]2,化简,得(m+1)2[(m﹣4)2﹣2]=0.
于是,得(m﹣4)2﹣2=0,m+1=0.
解得m1=4+![]() ,m2=4﹣
,m2=4﹣![]() ,m3=﹣1,
,m3=﹣1,
∵当m=﹣1时,P点与A点重合,
∴P1(4+![]() ,5+
,5+![]() ),P2(4﹣
),P2(4﹣![]() ,5﹣
,5﹣![]() );
);
②当PA=AQ时,(m+1)2+(m+1)2=(m+1)2+(m2﹣2m﹣3)2,化简,得(m+1)2(m﹣3﹣1)2=0,
于是,得(m﹣4)2=0,解得m4=4,m5=﹣1,
∴P3(4,5);
③当AQ=AP时,(m+1)2+(m2﹣2m﹣3)2=[m+1﹣(m2﹣2m﹣3)]2,化简,得(m+1)2[(m﹣4)2﹣2]=0.
于是,得(m2﹣2m﹣3)2=0.m+1=0,
解得m6=3,m7=﹣1,
∴P(3,4);
综上,存在点P,使以A、P、Q为顶点的三角形为等腰三角形,点P的坐标为P(4+![]() ,5+
,5+![]() )或(4﹣
)或(4﹣![]() ,5﹣
,5﹣![]() )或(4,5)或(3.4).
)或(4,5)或(3.4).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为了了解本校2 000名学生所需运动服尺码,在全校范围内随机抽取100名学生进行调查,这次抽样调查的样本容量是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的直径为8,且点P在⊙O内,则线段PO的长度( )
A.小于8 B.等于8 C.等于4 D.小于4
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(-2,-3)关于x轴的对称点为P1,点P1关于y轴的对称点为P2,则P2的坐标为( )
A. (-2,3) B. (-2,-3) C. (2,-3) D. (2,3)
-
科目: 来源: 题型:
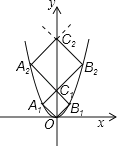
查看答案和解析>>【题目】如图,已知点A1,A2,…,A2011在函数y=x2位于第二象限的图象上,点B1,B2,…,B2011在函数y=x2位于第一象限的图象上,点C1,C2,…,C2011在y轴的正半轴上,若四边形OA1C1B1、C1A2C2B2,…,C2010A2011C2011B2011都是正方形,则正方形C2010A2011C2011B2011的边长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】“端午节”所示我国的传统佳节,民间历来有吃“粽子”的习俗,我市某食品厂为了解市民对去年销售较好的肉馅棕、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不用口味粽子的喜爱情况,在节前对某居民区进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).
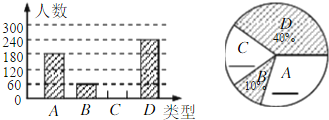
请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将两幅不完整的图补充完整;
(3)若居民区有8000人,请估计爱吃D粽的人数;
(4)若有外型完全相同的A、B、C、D粽各一个,煮熟后,小王吃了两个,用列表或画树状图的方法,求他第二个恰好吃到的是C粽的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点E在AD上,EC平分∠BED.
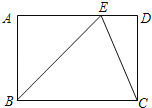
(1)△BEC是否为等腰三角形?为什么?
(2)若AB=a,∠ABE=45°,求BC的长.
相关试题

