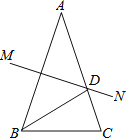
【题目】如图,AB=AC,AB的垂直平分线MN交AC于点D,若∠A=36°,则下列结论:①∠C=72°;②BD是∠ABC的平分线;③△ADB是等腰三角形;④△BCD的周长=AB+BC.正确是______(填序号).
参考答案:
【答案】①②③④
【解析】
①,△ABC中,∠A=36°,AB=AC,根据等腰三角形的性质与三角形内角和定理,即可求得∠C的度数;
对于②,分别求出∠ABD与∠DBC的度数,便可判断BD是否是∠ABC的平分线;
对于③,由线段垂直平分线的性质,得到AD=BD,即可判断△ABD的形状;
对于④,由AD=BD,AC=AB,根据三角形的周长周长公式及线段间的等量代换即可得△BCD的周长.
∵ AB=AC,
∴ ∠ABC=∠ACB.
∵ ∠BAC=36°,
∴ ∠ABC=∠ACB=72° .
故①正确;
∵ MN垂直平分AB,
∴ AD=BD,
∴ △ABD是等腰三角形,
∴ ∠BAC=∠ABD=36° .
∵ ∠ABD=36°,∠ABC=72°,
∴ ∠DBC=36°,
∴ BD平分∠ABC.
故②③正确;
∵ AD=BD,
∴ △BCD的周长=BD+CD+BC=AD+DC+BC=AC+BC.
∵ AC=AB,
∴ △BCD的周长=AB+BC.
故④正确.
综上可知,结论中成立的有①②③④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为了解全校学生到校上学的方式,在全校随机抽取了若干名学生进行问卷调查.问卷给出了五种上学方式供学生选择,每人只能选一项,且不能不选.同时把调查得到的结果绘制成如图所示的条形统计图和扇形统计图(均不完整).请根据图中提供的信息解答下列问题:
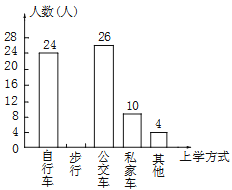
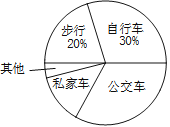
(1)在这次调查中,一共抽取了多少名学生?
(2)通过计算补全条形统计图;
(3)在扇形统计图中,“公交车”部分所对应的圆心角是多少度?
(4)若全校有1600名学生,估计该校乘坐私家车上学的学生约有多少名?
-
科目: 来源: 题型:
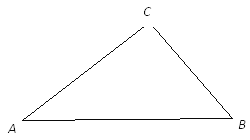
查看答案和解析>>【题目】如图,已知点D、E分别在△ACD的边AB和AC上,已知DE∥BC,DE=DB.
(1)请用直尺和圆规在图中画出点D和点E(保留作图痕迹,不要求写作法),并证明所作的线段DE是符合题目要求的;
(2)若AB=7,BC=3,请求出DE的长.
-
科目: 来源: 题型:
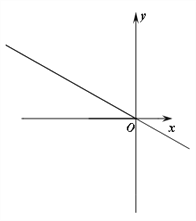
查看答案和解析>>【题目】已知二次函数
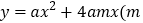 >0)的对称轴与x轴交于点B,与直线l:
>0)的对称轴与x轴交于点B,与直线l: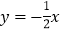 交于点C,点A是该二次函数图像与直线l在第二象限的交点,点D是抛物线的顶点,已知AC∶CO=1∶2,∠DOB=45°,△ACD的面积为2.
交于点C,点A是该二次函数图像与直线l在第二象限的交点,点D是抛物线的顶点,已知AC∶CO=1∶2,∠DOB=45°,△ACD的面积为2.(1) 求抛物线的函数关系式;
(2) 若点P为抛物线对称轴上的一个点,且∠POC=45°,求点P坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某品牌T恤专营批发店的T恤衫在进价基础上加价m%销售,每月销售额9万元,该店每月固定支出1.7万元,进货时还需付进价5%的其它费用.
(1)为保证每月有1万元的利润,m的最小值是多少?(月利润=总销售额-总进价-固定支
出-其它费用)
(2)经市场调研发现,售价每降低1%,销售量将提高6%,该店决定自下月起降价以促进销售,已知每件T恤原销售价为60元,问:在m取(1)中的最小值且所进T恤当月能够全部销售完的情况下,销售价调整为多少时能获得最大利润,最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某区为治理污水,需要铺设一段全长为 720 米的污水排放管道.“…”.设原计划每天铺设 x 米,可以列出方程
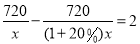 ,根据情景及所列方程,题中用“…”表示的缺失条件应补为( )
,根据情景及所列方程,题中用“…”表示的缺失条件应补为( )A.实际施工时每天的工作效率比原计划高 20%,结果提前 2 天完成任务;
B.原计划每天的工作效率比实际施工时低 20%,结果提前 2 天完成任务;
C.实际施工时每天的工作效率比原计划高 20%,结果延后 2 天完成任务;
D.原计划每天的工作效率比实际施工时低 20%,结果延后 2 天完成任务.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:矩形ABCD中,AB=4,BC=3,点M、N分别在边AB、CD上,直线MN交矩形对角线 AC于点E,将△AME沿直线MN翻折,点A落在点P处,且点P在射线CB上.
(1)如图1,当EP⊥BC时,求CN的长;
(2) 如图2,当EP⊥AC时,求AM的长;
(3) 请写出线段CP的长的取值范围,及当CP的长最大时MN的长.

相关试题

