Question

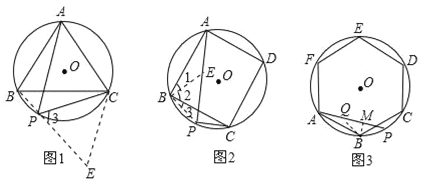
【题目】（1）己知，如图1，△ABC是⊙O的内接正三角形，点P为弧BC上一动点，请探究PA，PB，PC三者之间有何数量关系，并给予证明．

（2）如图2，四边形ABCD是⊙O的内接正方形，点P为弧BC上一动点，请探究PA，PB，PC三者之间有何数量关系，并给予证明．

（3）如图3，六边形ABCDEF是⊙O的内接正六边形，点P为弧BC上一动点，请探究PA、PB、PC三者之间有何数量关系，直接写出结论不需证明．

Answer 1

【答案】（1）PA=PB+PC；（2）PA=PC+PB；（3）PA=PB+PC．

【解析】

试题分析：（1）结论：PA=PB+PC．延长BP至E，使PE=PC，连接CE，证明△PCE是等边三角形．利用CE=PC，∠E=∠3=60°，∠EBC=∠PAC，得到△BEC≌△APC，所以PA=BE=PB+PC；

（2）结论：PA=PC+PB．过点B作BE⊥PB交PA于E，证明△ABE≌△CBP，所以PC=AE，可得PA=PC+PB．

（3）结论：PA=PB+PC．在AP上截取AQ=PC，连接BQ可证△ABQ≌△CBP，所以BQ=BP．又因为∠APB=30°．所以PQ=PB，PA=PQ+AQ=PB+PC．

试题解析：

（1）延长BP至E，使PE=PC，连接CE，如图1，∵A、B、P、C四点共圆，∴∠BAC+∠BPC=180°，∵∠BPC+∠EPC=180°，∴∠BAC=∠CPE=60°，PE=PC，∴△PCE是等边三角形，∴CE=PC，∠E=60°；

又∵∠BCE=60°+∠BCP，∠ACP=60°+∠BCP，∴∠BCE=∠ACP，∵△ABC、△ECP为等边三角形，∴CE=PC，AC=BC，在△BEC和△APC中，∵CE=PC，∠BEC=∠ACP，BC=AC，∴△BEC≌△APC（SAS），∴PA=BE=PB+PC；

（2）过点B作BE⊥PB交PA于E，如图2，∵∠1+∠2=∠2+∠3=90°

∴∠1=∠3，∴∠APB=45°，∴BP=BE，∴PE=PB，在△ABE和△CBP中，∵BE=BP，∠1=∠3，AB=BC，∴△ABE≌△CBP（SAS），∴PC=AE，∴PA=AE+PE=PC+PB；

（3）PA=PC+PB．

证明：过点B，作BM⊥AP，在AP上截取AQ=PC，连接BQ，如图3，∵∠BAP=∠BCP，AB=BC，在△ABQ和△CBP中，∵AQ=PC，∠BAP=∠BCP，AB=BC，∴△ABQ≌△CBP（SAS），∴BQ=BP，∴MP=QM，又∵∠APB=30°，∴cos30°=，∴PM=PB，∴PQ=PB，∴PA=PQ+AQ=PC+PB．