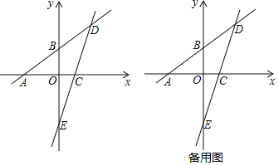
【题目】已知:如图,一次函数y=![]() x+3的图象分别与x轴、y轴相交于点A、B,且与经过点C(2,0)的一次函数y=kx+b的图象相交于点D,点D的横坐标为4,直线CD与y轴相交于点E.
x+3的图象分别与x轴、y轴相交于点A、B,且与经过点C(2,0)的一次函数y=kx+b的图象相交于点D,点D的横坐标为4,直线CD与y轴相交于点E.
(1)直线CD的函数表达式为______;(直接写出结果)
(2)在x轴上求一点P使△PAD为等腰三角形,直接写出所有满足条件的点P的坐标.
(3)若点Q为线段DE上的一个动点,连接BQ.点Q是否存在某个位置,将△BQD沿着直线BQ翻折,使得点D恰好落在直线AB下方的y轴上?若存在,求点Q的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)y=3x-6;(2)点P的坐标为(![]() ,0)或(6,0)或(-14,0)或(12,0);(3)存在,点Q的坐标为(
,0)或(6,0)或(-14,0)或(12,0);(3)存在,点Q的坐标为(![]() ,
,![]() )
)
【解析】
(1)求出D的坐标,即可求解;
(2)分PA=PD、当PA=AD、DP=AD三种情况,分别求解即可;
(3)利用BD=BD′,DQ=D′Q,即可求解.
解:(1)将点D的横坐标为4代入一次函数y=![]() x+3表达式,解得:y=6,即点D的坐标为(4,6),
x+3表达式,解得:y=6,即点D的坐标为(4,6),
将点C、D的坐标代入一次函数表达式y=kx+b得:![]()
解得: ![]()
故答案为:y=3x-6;
(2)①当PA=PD时,
点B是AD的中点,
故:过点B且垂直于AD的直线方程为:y=-![]() x+3,
x+3,
令y=0,则x=![]() ,
,
即点P的坐标为(![]() ,0);
,0);
②当PA=AD时,
AD=![]() =10,
=10,
故点P的坐标为(6,0)或(-14,0);
③当DP=AD时,
同理可得:点P的坐标为(12,0);
故点P的坐标为(![]() ,0)或(6,0)或(-14,0)或(12,0);
,0)或(6,0)或(-14,0)或(12,0);
(3)设翻转后点D落在y轴上的点为D′,设点Q的坐标为(x,3x-6),
则:BD=BD′,DQ=D′Q,
BD′=BD=![]() =5,故点D′的坐标为(0,-2),
=5,故点D′的坐标为(0,-2),
DQ2=D′Q2,即:x2+(3x-6+2)2=(x-4)2+(3x-6-6)2,
解得:x=![]() ,
,
故点Q的坐标为(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,把矩形纸片OABC放入直角坐标系xOy中,使OA、OC分别落在x、y轴的正半轴上,连接AC,且AC=4
 ,
, 
(1)求AC所在直线的解析式;
(2)将纸片OABC折叠,使点A与点C重合(折痕为EF),求折叠后纸片重叠部分的面积.
(3)求EF所在的直线的函数解析式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(–4,n),B(2,–4)是一次函数y=kx+b的图象和反比例函数
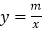 的图象的两个交点.
的图象的两个交点.(1)求反比例函数和一次函数的解析式;
(2)求直线AB与x轴的交点C的坐标及△AOB的面积;
(3)求不等式
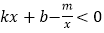 的解集(请直接写出答案).
的解集(请直接写出答案).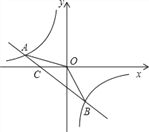
-
科目: 来源: 题型:
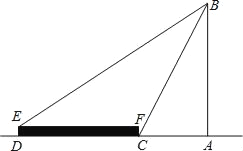
查看答案和解析>>【题目】如图,在一个平台远处有一座古塔,小明在平台底部的点C处测得古塔顶部B的仰角为60°,在平台上的点E处测得古塔顶部的仰角为30°.已知平台的纵截面为矩形DCFE,DE=2米,DC=20米,求古塔AB的高(结果保留根号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,给出下列的条件,能判断它是平行四边形的是( )
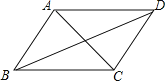
A. AB//CD, AD=BCB. ∠B=∠C,∠A=∠D
C. AB=AD, BC=CDD. AB=CD, AD=BC
-
科目: 来源: 题型:
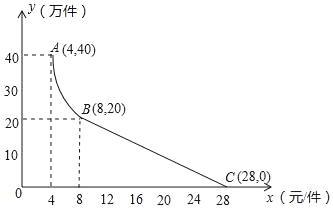
查看答案和解析>>【题目】月电科技有限公司用160万元,作为新产品的研发费用,成功研制出了一种市场急需的电子产品,已于当年投入生产并进行销售.已知生产这种电子产品的成本为4元/件,在销售过程中发现:每年的年销售量y(万件)与销售价格x(元/件)的关系如图所示,其中AB为反比例函数图象的一部分,BC为一次函数图象的一部分.设公司销售这种电子产品的年利润为s(万元).(注:若上一年盈利,则盈利不计入下一年的年利润;若上一年亏损,则亏损计作下一年的成本.)
(1)请求出y(万件)与x(元/件)之间的函数关系式;
(2)求出第一年这种电子产品的年利润s(万元)与x(元/件)之间的函数关系式,并求出第一年年利润的最大值.
(3)假设公司的这种电子产品第一年恰好按年利润s(万元)取得最大值时进行销售,现根据第一年的盈亏情况,决定第二年将这种电子产品每件的销售价格x(元)定在8元以上(x>8),当第二年的年利润不低于103万元时,请结合年利润s(万元)与销售价格x(元/件)的函数示意图,求销售价格x(元/件)的取值范围.
-
科目: 来源: 题型:
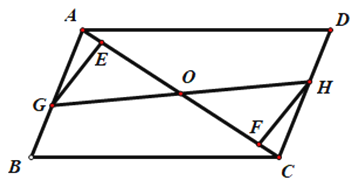
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点E、F在AC上,且AF=CE,点G、H分别在AB、CD上,且AG=CH,AC与GH相交于点O.
(1)求证:EG//FH;
(2)GH、EF互相平分.
相关试题

