【题目】CD是线段AB的垂直平分线,则∠CAD=∠CBD.请说明理由.
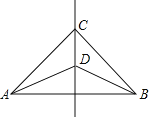
解:∵CD是线段AB的垂直平分线(已知),
∴AC=______,______=BD(______)
在△ADC和______中,
______=BC,
AD=______,
CD=______(______),
∴______≌______(______ ).
∴∠CAD=∠CBD (全等三角形的对应角相等).
参考答案:
【答案】BC AD 线段垂直平分线上的点到线段两端的距离相等 △BDC AC BD CD 公共边 △ADC △BDC SSS
【解析】
利用垂直平分线的性质,可以得到2个等腰三角形,△ACB和△ADB,再根据全等的判定,可以证得△ADC≌△BDC.
∵CD是线段AB的垂直平分线(已知),
∴AC=BC,AD=BD(线段垂直平分线上的点到线段两个端点的距离相等),
在△CBD和△CAD中
AC=BC
AD=BD
CD=CD
∴△CBD≌△CAD(SSS),
∴∠CAD=∠CBD(全等三角形的对应角相等),
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场投入13 800元资金购进甲、乙两种矿泉水共500箱,矿泉水的成本价和销售价如表所示:
类别/单价
成本价
销售价(元/箱)
甲
24
36
乙
33
48
(1)该商场购进甲、乙两种矿泉水各多少箱?
(2)全部售完500箱矿泉水,该商场共获得利润多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
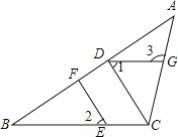
(1)CD与EF平行吗?为什么?
(2)如果∠1=∠2,CD平分∠ACB,且∠3=120°,求∠ACB与∠1的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R、S,若AQ=PQ,PR=PS,下面四个结论:①AS=AR;②QP∥AR;③△BRP≌△QSP;④AP垂直平分RS.其中正确结论的序号是 (请将所有正确结论的序号都填上).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E.
(1)若∠BAC=50°,求∠EDA的度数;
(2)求证:直线AD是线段CE的垂直平分线.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
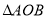 中,
中,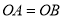 ,
,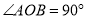 ,AD平分
,AD平分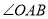 交OB于D,
交OB于D, 交AB于E,垂足为F.
交AB于E,垂足为F. 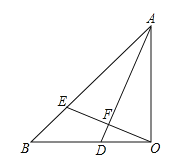
(1)求证:
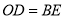 ;
; (2)若
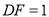 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,∠BAC的平分线AD交BC于点D,DE垂直平分AC,垂足为点E,∠BAD=29°,求∠B的度数.

相关试题

