【题目】某件商品的成本价为15元,据市场调查得知,每天的销量y(件)与价格x(元)有下列关系:
销售价格x | 20 | 25 | 30 | 50 |
销售量y | 15 | 12 | 10 | 6 |
(1)根据表中数据,在直角坐标系中描出实数对(x,y)的对应点,并画出图象;
(2)猜测确定y与x间的关系式;
(3)设总利润为W元,试求出W与x之间的函数关系式,若售价不超过30元,求出当日的销售单价定为多少时,才能获得最大利润?
参考答案:
【答案】(1)见解析 (2)![]() (3)当x=30时,w最大=150.
(3)当x=30时,w最大=150.
【解析】(1)根据描点法作函数的图象,先描点,连线即可得到答案,
(2)观察表中数据可得,x与y的积为常数,判断为反比例函数,根据数据,易得k的值,进而可得函数关系式,
(3)根据题意,易得关系式,根据反比例函数的单调性分析可得答案.
解:(1)根据描点法作函数的图象,先描点,连线即可得图象,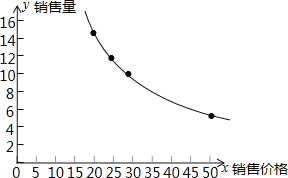
(2)观察表中数据可得,x与y得积为常数,判断为反比例函数,
根据数据,易得K=20×15=300,
故其解析式为y=![]() .
.
(3)w=(x-15) ![]() =300-
=300-![]() ;
;
当x≤30时,因为w随x增大而增大,
∴当x=30时,w最大=150.
“点睛”主要考查了函数的应用.解题的关键是根据实际意义列出函数关系式,从实际意义中找到对应的变量的值,利用待定系数法求出函数解析式,再根据自变量的值求算对应的函数值.本题尤其要注意分两种情况考虑,然后根据数据的规律舍去一种情况.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一段抛物线:y=﹣x(x﹣3)(0≤x≤3),记为C1,它与x轴交于点O,A1;
将C1绕点A1旋转180°得C2,交x轴于点A2;
将C2绕点A2旋转180°得C3,交x轴于点A3;
…
如此进行下去,直至得C13.若P(37,m)在第13段抛物线C13上,则m=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】作已知点关于某直线的对称点的第一步是( )
A.过已知点作一条直线与已知直线相交
B.过已知点作一条直线与已知直线垂直
C.过已知点作一条直线与已知直线平行
D.不确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知三条不同的直线a、b、c在同一平面内,下列四条命题:
①如果a∥b,a⊥c,那么b⊥c; ②如果b∥a,c∥a,那么b∥c;
③如果b⊥a,c⊥a,那么b⊥c;④如果b⊥a,c⊥a,那么b∥c.
其中真命题的是 . (填写所有真命题的序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】在下列四个命题中的逆命题中,是真命题的个数共有( )
①相等的角是对顶角;②等腰三角形腰上的高相等;③直角三角形的两个锐角互余;④全等三角形的三个角分别对应相等.
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
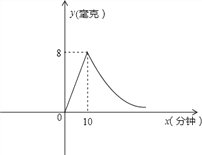
查看答案和解析>>【题目】为预防甲型H1N1流感,某校对教室喷洒药物进行消毒.已知喷洒药物时每立方米空气中的含药量y(毫克)与时间x(分钟)成正比,药物喷洒完后,y与x成反比例(如图所示).现测得10分钟喷洒完后,空气中每立方米的含药量为8毫克.
(1)求喷洒药物时和喷洒完后,y关于x的函数关系式;
(2)若空气中每立方米的含药量低于2毫克学生方可进教室,问消毒开始后至少要经过多少分钟,学生才能回到教室?
(3)如果空气中每立方米的含药量不低于4毫克,且持续时间不低于10分钟时,才能杀灭流感病毒,那么此次消毒是否有效?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=x+1与反比例函数y=
 的图象交于A,B两点,已知点A的坐标为(1,a),点B的坐标为(b,﹣1).
的图象交于A,B两点,已知点A的坐标为(1,a),点B的坐标为(b,﹣1).(1)求此反比例函数的解析式;
(2)当一次函数y=x+1的值大于反比例函数y=
 的值时,求自变量x的取值范围.
的值时,求自变量x的取值范围.
相关试题

