【题目】如图,在6×8的网格中,每个小正方形的边长均为1,点O和△ABC的顶点均为小正方形的顶点.

(1)在图中△ABC的内部作△A′B′C′,使△A′B′C′和△ABC位似,且位似中心为点O,位似比为1:2;
(2)连接(1)中的AA′,则线段AA′的长度是________.
参考答案:
【答案】(1)作图见解析;(2)![]() .
.
【解析】试题分析:
(1)连接OA,分别作出OA、OB、OC的中点A′、B′、C′,再顺次连接这三点即可得到所求三角形;
(2)由点O、点A都是格点结合图形和勾股定理可求得得AO的长度,由点OA′:OA=1:2即可求得AA′的长度.
试题解析:
(1)如下图,△A′B′C′为所作;
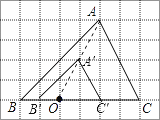
(2)由图结合勾股定理可得:AO=![]() ,
,
∵点OA′:OA=1:2,
∴OA′=![]() OA=
OA=![]() ,
,
∴AA′=OA-OA′=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】探寻“勾股数”:直角三角形三边长是整数时我们称之为“勾股数”,勾股数有多少?勾股数有规律吗?
(1)请你写出两组勾股数.
(2)试构造勾股数.构造勾股数就是要寻找3个正整数,使他们满足“两个数的平方和(或差)等于第三数的平方”,即满足以下形式:
① 2+ 2= 2;或② 2﹣ 2= 2
③要满足以上①、②的形式,不妨从乘法公式入手.我们已经知道③(x+y)2﹣(x﹣y)2=4xy.如果等式③右边也能写成 2的形式,就能符合②的形式.
因此不妨设x=m2,y=n2,(m、n为任意正整数,m>n),请你写出含m、n的这三个勾股数并证明它们是勾股数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,A、B、C、D在同一直线上,AB=CD,DE∥AF,若要使△ACF≌△DBE,则还需要补充一个条件:_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图为二次函数y=ax2+bx+c的图象,在下列说法中:
①ac<0;
②方程ax2+bx+c=0的根是x1=﹣1,x2=3;
③a+b+c>0;
④当x>1时,y随着x的增大而增大.
正确的说法有________.(请写出所有正确的序号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,E是AD的中点,延长CB到点F,使
 ,连接BE、AF.
,连接BE、AF.(1)完成画图并证明四边形AFBE是平行四边形;
(2)若AB=6,AD=8,∠C=60°,求BE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为加强学生身体锻炼,某校开展体育“大课间”活动,学校决定在学生中开设A:篮球,B:立定跳远,C:跳绳,D:跑步,E:排球五种活动项目.为了了解学生对五种项目的喜欢情况,随机抽取了部分学生进行调查,并将调查结果绘制成如图所示的两个统计图.请结合图中的信息解答下列问题:
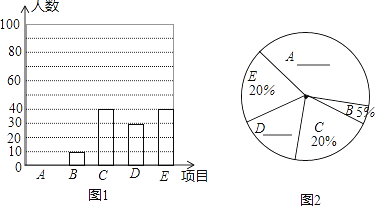
(1)在这项调查中,共调查了_______名学生;
(2)请将两个统计图补充完整;
(3)若该校有1200名在校学生,请估计喜欢排球的学生大约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB∥CD,∠1=∠2,DB=DC.
(1)求证:△ABD≌△EDC;
(2)若∠A=135°,∠BDC=30°,求∠BCE的度数.

相关试题

