【题目】将抛物线c1: ![]() 沿x轴翻折,得到抛物线c2 , 如图1所示.
沿x轴翻折,得到抛物线c2 , 如图1所示.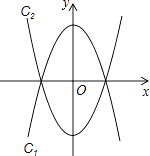
(1)请直接写出抛物线c2的表达式;
(2)现将抛物线c1向左平移m个单位长度,平移后得到新抛物线的顶点为M,与x轴的交点从左到右依次为A、B;将抛物线c2向右也平移m个单位长度,平移后得到新抛物线的顶点为N,与x轴的交点从左到右依次为D、E.
①当B、D是线段AE的三等分点时,求m的值;②在平移过程中,是否存在以点A、N、E、M为顶点的四边形是矩形的情形?若存在,请求出此时m的值;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:y= ![]() x2﹣
x2﹣ ![]()
(2)
解:①如图1,令﹣ ![]() x2+
x2+ ![]() =0,得x1=﹣1,x2=1
=0,得x1=﹣1,x2=1
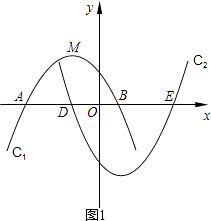
则拋物线c1与x轴的两个交点坐标为(﹣1,0),(1,0).
∴A(﹣1﹣m,0),B(1﹣m,0).
同理可得:D(﹣1+m,0),E(1+m,0).
当AD= ![]() AE时,
AE时,
(﹣1+m)﹣(﹣1﹣m)= ![]() [(1+m)﹣(﹣1﹣m)],
[(1+m)﹣(﹣1﹣m)],
∴m= ![]() .
.
当BD= ![]() AE时,
AE时,
(﹣1+m)﹣(1﹣m)= ![]() [(1+m)﹣(﹣1﹣m)],
[(1+m)﹣(﹣1﹣m)],
∴m=2.
故当B,D是线段AE的三等分点时,m= ![]() 或2.
或2.
②存在.
理由:如图2,连接AN,NE,EM,MA.

依题意可得:M(﹣m, ![]() ),N(m,﹣
),N(m,﹣ ![]() ).
).
即M,N关于原点O对称,
∴OM=ON.
∵A(﹣1﹣m,0),E(1+m,0),
∴A,E关于原点O对称,
∴OA=OE
∴四边形ANEM为平行四边形.
∵AM2=(﹣m+1+m)2+( ![]() )2=4,
)2=4,
ME2=(1+m+m)2+( ![]() )2=4m2+4m+4,
)2=4m2+4m+4,
AE2=(1+m+1+m)2=4m2+8m+4,
若AM2+ME2=AE2,则4+4m2+4m+4=4m2+8m+4,
∴m=1,
此时△AME是直角三角形,且∠AME=90°.
∴当m=1时,以点A,N,E,M为顶点的四边形是矩形.
【解析】(1)根据翻折的性质可求拋物线c2的表达式;(2)①求出拋物线c1与x轴的两个交点坐标,分当AD= ![]() AE时,当BD=
AE时,当BD= ![]() AE时两种情况讨论求解;②存在.理由:如图2,连接AN,NE,EM,MA.根据矩形的判定即可得出.
AE时两种情况讨论求解;②存在.理由:如图2,连接AN,NE,EM,MA.根据矩形的判定即可得出.
【考点精析】根据题目的已知条件,利用二次函数的性质的相关知识可以得到问题的答案,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果三角形的两边长分别是 3 和 6, 且第三边是偶数, 那么第三边长为______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD内接于⊙O,AB是⊙O的直径,AC和BD相交于点E,且DC2=CECA.
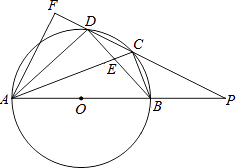
(1)求证:BC=CD;
(2)分别延长AB,DC交于点P,过点A作AF⊥CD交CD的延长线于点F,若PB=OB,CD=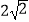 ,求DF的长.
,求DF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形ABCD,P为射线AB上的一点,以BP为边作正方形BPEF,使点F在线段CB的延长线上,连接EA、EC.

(1)如图1,若点P在线段AB的延长线上,求证:EA=EC;
(2)若点P在线段AB上.
①如图2,连接AC,当P为AB的中点时,判断△ACE的形状,并说明理由;
②如图3,设AB=a,BP=b,当EP平分∠AEC时,求a:b及∠AEC的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】点 M(-6,2)在第____________象限.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABN和△ACM位置如图所示,AB=AC,AD=AE,∠1=∠2.
(1)求证:BD=CE;
(2)求证:∠M=∠N.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在2017年十堰市初中体育中考中,随意抽取某校5位同学跳远的记录分别为:158,160,154,158,170,则由这组数据得到的结论错误的是( )
A.平均数为160
B.中位数为158
C.众数为158
D.方差为20.3
相关试题

