【题目】如图,CE是⊙O的直径,D为⊙O上一点,过点D作⊙O的切线,交CE延长线于点A,连接DE,过点O作OB∥ED,交AD的延长线于点B,连接BC.
(1)求证:直线BC是⊙O的切线;
(2)若AE=2,tan∠DEO= ![]() ,求AO的长.
,求AO的长.
参考答案:
【答案】
(1)证明:连接OD,
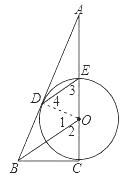
∵DE∥BO,
∴∠1=∠4,∠2=∠3,
∵OD=OE,
∴∠3=∠4,
∴∠1=∠2,
在△DOB与△COB中,
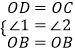 ,
,
∴△DOB≌△COB,
∴∠OCB=∠ODB,
∵BD切⊙O于点D,
∴∠ODB=90°,
∴∠OCB=90°,
∴AC⊥BC,
∴直线BC是⊙O的切线
(2)解:∵∠DEO=∠2,
∴tan∠DEO=tan∠2= ![]() ,
,
设OC=r,BC= ![]() r,
r,
由(1)证得△DOB≌△COB,
∴BD=BC= ![]() r,
r,
由切割线定理得:AD2=AEAC=2(2+r),
∴AD=2 ![]() ,
,
∵DE∥BO,
∴ ![]() ,
,
∴ ![]() ,
,
∴r=1,
∴AO=3.
【解析】(1)要证明直线BC是⊙O的切线,连接OD,根据已知先证明∠1=∠2,再证明△DOB≌△COB,得出∠OCB=∠ODB,然后根据切线的性质证明∠OCB=90°,即可证得结论。
(2)利用tan∠DEO= ![]() ,得出 tan∠2=
,得出 tan∠2= ![]() ,由△DOB≌△COB得出BD=BC,再根据切割线定理,证得AD2=AEAC,可表示出AD的长,再由DE∥BO,得对应线段成比例,求出r的长,即可求出AO的长。
,由△DOB≌△COB得出BD=BC,再根据切割线定理,证得AD2=AEAC,可表示出AD的长,再由DE∥BO,得对应线段成比例,求出r的长,即可求出AO的长。
【考点精析】利用平行线分线段成比例和相似三角形的判定与性质对题目进行判断即可得到答案,需要熟知三条平行线截两条直线,所得的对应线段成比例;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列命题中:①过一点有且只有一条直线与已知直线平行;②平方根与立方根相等的数有
 和
和 ;③在同一平面内,如果
;③在同一平面内,如果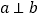 ,
, ,则
,则 ;④直线
;④直线 外一点
外一点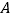 与直线
与直线 上各点连接而成的所有线段中,最短线段的长是
上各点连接而成的所有线段中,最短线段的长是 ,则点
,则点 到直线
到直线 的距离是
的距离是 ;⑤无理数包括正无理数、零和负无理数.其中真命题的个数是( )
;⑤无理数包括正无理数、零和负无理数.其中真命题的个数是( )A.
 个B.
个B.  个C.
个C.  个D.
个D.  个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线
 经过第一象限内一点A,且OA=4过点A作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD,则点C的坐标为( )
经过第一象限内一点A,且OA=4过点A作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD,则点C的坐标为( )
A. (
 ,2) B. (
,2) B. ( ,1)
,1)C. (-2,
 ) D. (-1,
) D. (-1, )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB⊥BC于点B,DC⊥BC于点C,DE平分∠ADC交BC于点E,点F为线段CD延长线上一点,∠BAF=∠EDF.
(1)求证:∠DAF=∠F;
(2)在不添加任何辅助线的情况下,请直接写出所有与∠CED互余的角.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
小天在学习锐角三角函数中遇到这样一个问题:在Rt△ABC中,∠C=90°,∠B=22.5°,则tan22.5°=
小天根据学习几何的经验,先画出了几何图形(如图1),他发现22.5°不是特殊角,但它是特殊角45°的一半,若构造有特殊角的直角三角形,则可能解决这个问题.于是小天尝试着在CB边上截取CD=CA,连接AD(如图2),通过构造有特殊角(45°)的直角三角形,经过推理和计算使问题得到解决.
请回答:tan22.5°= .
参考小天思考问题的方法,解决问题:
如图3,在等腰△ABC 中,AB=AC,∠A=30°,请借助△ABC,构造出15°的角,并求出该角的正切值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.

(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,
 为坐标原点,点
为坐标原点,点 和点
和点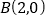 是坐标轴上两点,点
是坐标轴上两点,点 为坐标轴上一点,若三角形
为坐标轴上一点,若三角形 的面积为
的面积为 ,则
,则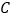 点坐标为__________.
点坐标为__________.
相关试题

