【题目】如图,AB∥CD.∠1=∠2,∠3=∠4,试说明 AD∥BE,请你将下面解答过程填写完整.

解:∵AB∥CD,
∴∠4= ( )
∵∠3=∠4
∴∠3= (等量代换)
∵∠1=∠2
∴∠1+∠CAF=∠2+∠CAE 即∠BAE= .
∴∠3= ( )
∴AD∥BE( ).
参考答案:
【答案】∠BAE;两直线平行,同位角相等;∠BAE;∠CAD;∠CAD;等量代换;内错角相等,两直线平行.
【解析】
根据平行线的性质得出∠4=∠BAE,由此∠3=∠BAE,根据∠2=∠1可得∠BAE=∠CAD,从而得出∠3=∠CAD,根据平行线的判定定理得出即可.
解:∵AB∥CD,
∴∠4= ∠BAE ( 两直线平行,同位角相等 ),
∵∠3=∠4,
∴∠3= ∠BAE (等量代换),
∵∠1=∠2,
∴∠1+∠CAF=∠2+∠CAE,
即∠BAE= ∠CAD ,
∴∠3= ∠CAD ( 等量代换 ),
∴AD∥BE( 内错角相等,两直线平行 ).
-
科目: 来源: 题型:
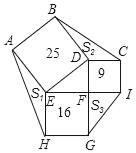
查看答案和解析>>【题目】如图,正方形ABDE、CDFI、EFGH的面积分别为25、9、16,△AEH、△BDC、△GFI的面积分别为S1、S2、S3,则S1+S2+S3=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一架梯子AB长13米,斜靠在一面墙上,梯子底端离墙5米.(1)这个梯子的顶端距地面有多高?(2)如果梯子的顶端下滑了5米,那么梯子的底端在水平方向滑动了多少米?

-
科目: 来源: 题型:
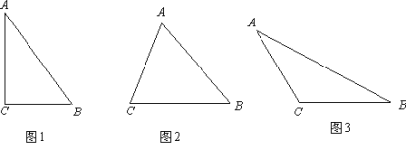
查看答案和解析>>【题目】△ABC中,BC=a,AC=b,AB=c,若∠C=90°,如图(1),根据勾股定理,则a2+b2=c2,若△ABC不是直角三角形,如图(2)和图(3),请你类比勾股定理,试猜想a2+b2与c2的关系,并证明你的结论.
-
科目: 来源: 题型:
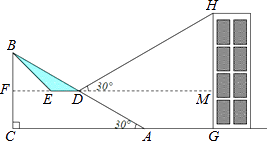
查看答案和解析>>【题目】为方便市民通行,某广场计划对坡角为30°,坡长为60米的斜坡AB进行改造,在斜坡中点D处挖去部分坡体(阴影表示),修建一个平行于水平线CA的平台DE和一条新的斜坡BE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=
 AC,连接AE交OD于点F,连接CE、OE.
AC,连接AE交OD于点F,连接CE、OE.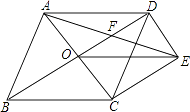
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC,CD⊥AB于D点,M,N是AC,BC上的动点,且∠MDN=90°,下列结论:①AM=CN;②四边形MDNC的面积为定值;③AM2+BN2=MN2;④NM平分∠CND.其中正确的是 ( )

A. ①②③ B. ①②④ C. ①③④ D. ①②③④
相关试题

