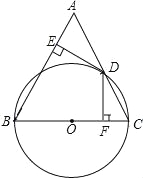
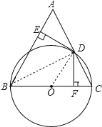
【题目】如图,在△ABC中,AB=BC,以BC为直径的⊙O交AC于点D,过点D作DE⊥AB,DF⊥BC,垂足分别为E、F.
(1)求证:ED是⊙O的切线;
(2)若DF=3![]() ,cosA=
,cosA=![]() ,求⊙O的直径.
,求⊙O的直径.
参考答案:
【答案】(1)证明见解析;
(2)⊙O的直径为![]() .
.
【解析】
试题分析:(1)连结OD、BD,先根据圆周角定理得到∠BDC=90°,再根据等腰三角形的性质得到AD=CD,则可判断OD为△ABC的中位线,所以OD∥AB,加上DE⊥AB,则DE⊥OD,然后根据切线的判定定理得ED是⊙O的切线;
(2)根据等腰三角形的性质由AB=AC得到∠A=∠C,在Rt△CFD中利用余弦定理得到cosC=![]() =cosA=
=cosA=![]() ,则可设CF=2x,CD=3x,利用勾股定理得到DF=
,则可设CF=2x,CD=3x,利用勾股定理得到DF=![]() x,所以
x,所以![]() x=3
x=3![]() ,解得x=3,于是计算出CD=9,然后在Rt△BCD中利用余弦的定义计算出BC的长即可.
,解得x=3,于是计算出CD=9,然后在Rt△BCD中利用余弦的定义计算出BC的长即可.
试题解析:(1)连结OD、BD,∵BC为直径,∴∠BDC=90°,∴BD⊥AC,
而BA=BC,∴AD=CD,而OB=OC,∴OD为△ABC的中位线,∴OD∥AB,
∵DE⊥AB,∴DE⊥OD,∴ED是⊙O的切线;
(2)∵AB=AC,∴∠A=∠C,在Rt△CFD中,cosC=![]() =cosA=
=cosA=![]() ,
,
设CF=2x,CD=3x,
∴DF=![]() =
=![]() x,∴
x,∴![]() x=3
x=3![]() ,解得x=3,∴CD=9,
,解得x=3,∴CD=9,
在Rt△BCD中,∵cosC=![]() =
=![]() ,∴BC=
,∴BC=![]() ×9=
×9=![]() ,
,
即⊙O的直径为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】五一期间,新华商场贴出促销海报.在商场活动期间,王莉同学随机调查了部分参与活动的顾客,并将调查结构绘制了两幅不完整的统计图.
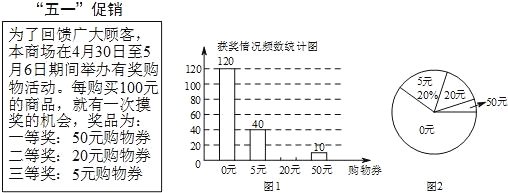
请你根据图中的信息回答下列问题:
(1)王莉同学随机调查的顾客有 人;
(2)请将统计图1补充完整;
(3)在统计图2中,“0元”部分所对应的圆心角是 度;
(4)若商场每天约有2 000人次摸奖,请估算商场一天送出的购物券总金额是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个数的立方是它本身,那么这个数是( )
A.0
B.0或1
C.-1或1
D.0或1或-1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到(0,1),然后接着按图中箭头所示方向跳动:即(0,0)→(0,1) →(1,1)→(1,0)→…,且每秒跳动一个单位,那么第35秒时跳蚤所在位置的坐标是( )

A.(4,0)
B.(5,0)
C.(0,5)
D.(5,5) -
科目: 来源: 题型:
查看答案和解析>>【题目】直线MN与线段AB相交于点O.点C,点D分别为射线ON,OM上两点,且满足∠ACN=∠ODB=45°.
【特殊发现】
(1)如图1,若AO=OB,当点C与点O重合时,此时AO与BD的数量关系为 ,AO与BD的位置关系为 ;
【拓展探究】
(2)将图1中的MN绕点O顺时针旋转α°,(0<α<45),如图2所示,若AO=OB,求证:AC=BD,AC⊥BD;
【解决问题】
(3)如图3,若kAO=OB,求
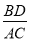 的值.
的值.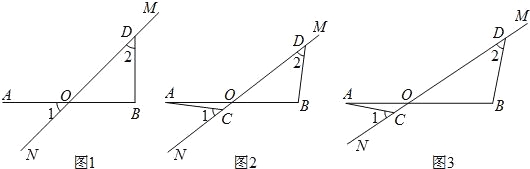
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个有理数的正偶次幂是非负数,那么这个数是( )
A.正数
B.负数
C.非负数
D.任何有理数 -
科目: 来源: 题型:
查看答案和解析>>【题目】某校教师假期外出考察4天,已知这四天的日期之和是38,那么这四天的日期分别是______________.
相关试题

