【题目】用配方法解下列方程时,配方有错误的是( )
A.x2﹣2x﹣99=0化为(x﹣1)2=100
B.x2+8x+9=0化为(x+4)2=25
C.2t2﹣7t﹣4=0化为(t﹣ ![]() )2=
)2= ![]()
D.3x2﹣4x﹣2=0化为(x﹣ ![]() )2=
)2= ![]()
参考答案:
【答案】B
【解析】解:A、∵x2﹣2x﹣99=0,∴x2﹣2x=99,∴x2﹣2x+1=99+1,∴(x﹣1)2=100,故A选项正确.
B、∵x2+8x+9=0,∴x2+8x=﹣9,∴x2+8x+16=﹣9+16,∴(x+4)2=7,故B选项错误.
C、∵2t2﹣7t﹣4=0,∴2t2﹣7t=4,∴t2﹣ ![]() t=2,∴t2﹣
t=2,∴t2﹣ ![]() t+
t+ ![]() =2+
=2+ ![]() ,∴(t﹣
,∴(t﹣ ![]() )2=
)2= ![]() ,故C选项正确.
,故C选项正确.
D、∵3x2﹣4x﹣2=0,∴3x2﹣4x=2,∴x2﹣ ![]() x=
x= ![]() ,∴x2﹣
,∴x2﹣ ![]() x+
x+ ![]() =
= ![]() +
+ ![]() ,∴(x﹣
,∴(x﹣ ![]() )2=
)2= ![]() .故D选项正确.
.故D选项正确.
所以答案是:B.
【考点精析】本题主要考查了配方法的相关知识点,需要掌握左未右已先分离,二系化“1”是其次.一系折半再平方,两边同加没问题.左边分解右合并,直接开方去解题才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校在商场购买甲、乙两种不同足球,购买甲种足球共花费2000元,购买乙种足球共花费1400元,购买甲种足球数量是购买乙种足球数量的2倍,且购买一个乙种足球比购买一个甲种足球多花20元.
(1)求购买一个甲种足球、一个乙种足球各需多少元?
(2)为响应“足球进校园”的号召,这所学校决定再次购买甲、乙两种足球共50个.恰逢该商场对两种足球的售价进行调整,甲种足球售价比第一次购买时提高了10%,乙种足球售价比第一次购买时降低了10%,如果此次购买甲、乙两种足球的总费用不超过2900元,那么这所学校最多可购买多少个乙种足球?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
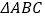 是边长为
是边长为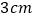 的等边三角形,动点
的等边三角形,动点 以
以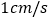 的速度从点
的速度从点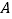 出发,沿线段
出发,沿线段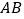 向点
向点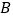 运动.
运动.(1)如图甲,设点
 的运动时间为
的运动时间为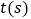 ,那么
,那么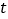 为何值时,
为何值时,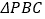 是直角三角形?
是直角三角形?(2)若另一动点
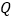 从点
从点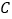 出发,沿射线
出发,沿射线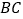 方向运动,连接
方向运动,连接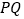 交
交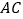 于点
于点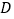 ,如果动点
,如果动点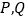 都以
都以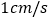 的速度同时出发.
的速度同时出发.①如图乙,设运动时间为
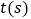 ,那么
,那么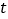 为何值时,
为何值时,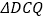 是等腰三角形?
是等腰三角形?②如图丙,连接
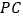 ,请你猜想:在点
,请你猜想:在点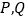 的运动过程中,
的运动过程中,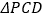 和
和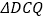 的面积有什么关系?并说明理由.
的面积有什么关系?并说明理由.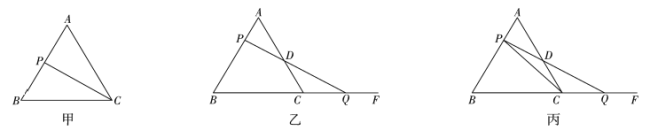
-
科目: 来源: 题型:
查看答案和解析>>【题目】若﹣
 a≥b,则a≤﹣2b,其根据是( )
a≥b,则a≤﹣2b,其根据是( )
A.不等式的两边都加上(或减去)同一个整式,不等号的方向不变
B.不等式的两边都乘(或除以)同一个正数,不等号的方向不变
C.不等式的两边都乘(或除以)同一个负数,不等号的方向改变
D.以上答案均不对 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将正方形对折后展开(图④是连续两次对折后再展开),再按图示方法折叠,能够得到一个直角三角形(阴影部分),且它的一条直角边等于斜边的一半.这样的图形有( )
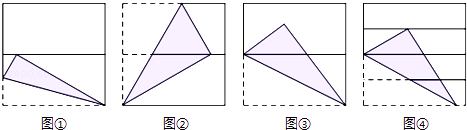
A.4个
B.3个
C.2个
D.1个 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列结沦中,错误的有( )
①Rt△ABC中,已知两边分别为3和4,则第三边的长为5;②三角形的三边分别为a、b、c,若a2+b2=c2,则∠A=90°;③若△ABC中,∠A:∠B:∠C=1:5:6,则这个三角形是一个直角三角形;④若(x﹣y)2+M=(x+y)2成立,则M=4xy.
A. 0个 B. 1个 C. 2个 D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标为(1,n),与y轴的交点在(0,2)、(0,3)之间(包含端点).有下列结论:
①当x>3时,y<0;②3a+b>0;③﹣1≤a≤﹣ ;④
;④  ≤n≤4.
≤n≤4.
其中正确的是( )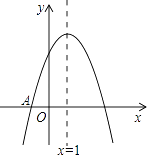
A.①②
B.③④
C.①③
D.①③④
相关试题

