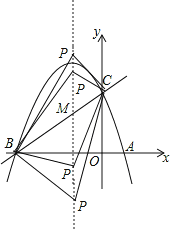
【题目】如图,已知抛物线![]() 的对称轴x=-1,且抛物线经过
的对称轴x=-1,且抛物线经过![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.

⑴.若直线![]() 经过
经过![]() 两点,求直线
两点,求直线![]() 所在直线的解析式;
所在直线的解析式;
⑵.抛物线的对称轴x=-1上找一点![]() ,使点
,使点![]() 到点
到点![]() 的距离与到点
的距离与到点![]() 的距离之和最小,求出此点
的距离之和最小,求出此点![]() 的坐标;
的坐标;
⑶.设点![]() 为抛物线的对称轴x=-1上的一个动点,求使△
为抛物线的对称轴x=-1上的一个动点,求使△![]() 为直角三角形的点
为直角三角形的点![]() 的坐标.
的坐标.
参考答案:
【答案】(1)y=x+3;(2)(-1,2);(3)(-1,-2)或(-1,4)或(-1,![]() )或(-1,
)或(-1,![]() ).
).
【解析】
试题分析:(1)先把点A,C的坐标分别代入抛物线解析式得到a和b,c的关系式,再根据抛物线的对称轴方程可得a和b的关系,再联立得到方程组,解方程组,求出a,b,c的值即可得到抛物线解析式;把B、C两点的坐标代入直线y=mx+n,解方程组求出m和n的值即可得到直线解析式;
(2)设直线BC与对称轴x=-1的交点为M,则此时MA+MC的值最小.把x=-1代入直线y=x+3得y的值,即可求出点M坐标;
(3)设P(-1,t),又因为B(-3,0),C(0,3),所以可得BC2=18,PB2=(-1+3)2+t2=4+t2,PC2=(-1)2+(t-3)2=t2-6t+10,再分三种情况分别讨论求出符合题意t值即可求出点P的坐标.
试题解析:(1)依题意得: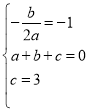 ,
,
解之得: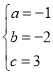 ,
,
∴抛物线解析式为y=-x2-2x+3
∵对称轴为x=-1,且抛物线经过A(1,0),
∴把B(-3,0)、C(0,3)分别代入直线y=mx+n,
得![]() ,
,
解之得:![]() ,
,
∴直线y=mx+n的解析式为y=x+3;
(2)设直线BC与对称轴x=-1的交点为M,则此时MA+MC的值最小.
把x=-1代入直线y=x+3得,y=2,
∴M(-1,2),
即当点M到点A的距离与到点C的距离之和最小时M的坐标为(-1,2);
(3)设P(-1,t),
又∵B(-3,0),C(0,3),
∴BC2=18,PB2=(-1+3)2+t2=4+t2,PC2=(-1)2+(t-3)2=t2-6t+10,
①若点B为直角顶点,则BC2+PB2=PC2即:18+4+t2=t2-6t+10解之得:t=-2;
②若点C为直角顶点,则BC2+PC2=PB2即:18+t2-6t+10=4+t2解之得:t=4,
③若点P为直角顶点,则PB2+PC2=BC2即:4+t2+t2-6t+10=18解之得:t1=![]() ,t2=
,t2=![]() ;
;
综上所述P的坐标为(-1,-2)或(-1,4)或(-1,![]() )或(-1,
)或(-1,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=52°,∠ABC与∠ACB的角平分线交于D1,∠ABD1与∠ACD1的角平分线交于点D2,依此类推,∠ABD4与∠ACD4的角平分线交于点D5,则∠BD5C的度数是 ( )

A. 56° B. 60° C. 68° D. 94°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).
①图2中的阴影部分的面积为 ;
②观察图2请你写出 (a+b)2、(a﹣b)2、ab之间的等量关系是 ;
③根据(2)中的结论,若x+y=5,xy=
 ,则(x﹣y)2= ;
,则(x﹣y)2= ;④实际上通过计算图形的面积可以探求相应的等式.
如图3,你发现的等式是 .

-
科目: 来源: 题型:
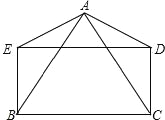
查看答案和解析>>【题目】如图,AB=AC,AD=AE,DE=BC,且∠BAD=∠CAE.求证:四边形BCDE是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD是△ABC的角平分线,DE∥BC,交AB于点E,∠A=50°,∠BDC=75°.求∠BED的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我国计划在2020年左右发射火星探测卫星,据科学研究测量,火星距离地球的最近距离约为5500万千米,这个数据用科学计数法表示为
A. 5.5×106 B. 5.5×107 C. 55×107 D. 0.55×108
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个正方形的面积是6平方厘米,则这个正方形的边长等于厘米.
相关试题

