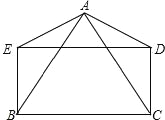
【题目】如图,AB=AC,AD=AE,DE=BC,且∠BAD=∠CAE.求证:四边形BCDE是矩形.
参考答案:
【答案】证明见解析.
【解析】
试题分析:求出∠BAE=∠CAD,证△BAE≌△CAD,推出∠BEA=∠CDA,BE=CD,得出平行四边形BCDE,根据平行线性质得出∠BED+∠CDE=180°,求出∠BED,根据矩形的判定求出即可.
试题解析:∵∠BAD=∠CAE,
∴∠BAD-∠BAC=∠CAE-∠BAC,
∴∠BAE=∠CAD,
∵在△BAE和△CAD中

∴△BAE≌△CAD(SAS),
∴∠BEA=∠CDA,BE=CD,
∵DE=CB,
∴四边形BCDE是平行四边形,
∵AE=AD,
∴∠AED=∠ADE,
∵∠BEA=∠CDA,
∴∠BED=∠CDE,
∵四边形BCDE是平行四边形,
∴BE∥CD,
∴∠CDE+∠BED=180°,
∴∠BED=∠CDE=90°,
∴四边形BCDE是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各语句:①对顶角相等吗?②延长线段AB;③内错角相等;④垂线段最短.其中真命题有( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=52°,∠ABC与∠ACB的角平分线交于D1,∠ABD1与∠ACD1的角平分线交于点D2,依此类推,∠ABD4与∠ACD4的角平分线交于点D5,则∠BD5C的度数是 ( )

A. 56° B. 60° C. 68° D. 94°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).
①图2中的阴影部分的面积为 ;
②观察图2请你写出 (a+b)2、(a﹣b)2、ab之间的等量关系是 ;
③根据(2)中的结论,若x+y=5,xy=
 ,则(x﹣y)2= ;
,则(x﹣y)2= ;④实际上通过计算图形的面积可以探求相应的等式.
如图3,你发现的等式是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
 的对称轴x=-1,且抛物线经过
的对称轴x=-1,且抛物线经过 两点,与
两点,与 轴交于点
轴交于点 .
.
⑴.若直线
 经过
经过 两点,求直线
两点,求直线 所在直线的解析式;
所在直线的解析式;⑵.抛物线的对称轴x=-1上找一点
 ,使点
,使点 到点
到点 的距离与到点
的距离与到点 的距离之和最小,求出此点
的距离之和最小,求出此点 的坐标;
的坐标;⑶.设点
 为抛物线的对称轴x=-1上的一个动点,求使△
为抛物线的对称轴x=-1上的一个动点,求使△ 为直角三角形的点
为直角三角形的点 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD是△ABC的角平分线,DE∥BC,交AB于点E,∠A=50°,∠BDC=75°.求∠BED的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我国计划在2020年左右发射火星探测卫星,据科学研究测量,火星距离地球的最近距离约为5500万千米,这个数据用科学计数法表示为
A. 5.5×106 B. 5.5×107 C. 55×107 D. 0.55×108
相关试题

