【题目】为庆祝“元旦”,光明学校统一组织合唱比赛,七、八年级共92人(其中七年级的人数多于八年级的人数,且七年级的人数不足90人)准备统一购买服装参加比赛.下面是某服装厂给出服装的价格表:
购买服装的套数 | 1套至45套 | 46套至90套 | 91套以上(含91套) |
每套服装的价格 | 60元 | 50元 | 40元 |
购买服装的套数 | 1套至45套 | 46套至90套 | 91套以上(含91套) |
每套服装的价格 | 60元 | 50元 | 40元 |
(1)如果两个年级分别单独购买服装一共应付5000元,求七、八年级各有多少学生参加合唱比赛;
(2)如果七年级参加合唱比赛的学生中,有10名同学抽调去参加绘画比赛,不能参加合唱比赛,请你为两个年级设计一种最省钱的购买服装方案.
参考答案:
【答案】(1)七年级有52人,则八年级有40人.(2)最省钱的购买方案是:两个年级联合购买91套服装(即比实际人数多买9套).
【解析】
(1)七年级的人数多于八年级的人数,可得七年级服装的单价为50,八年级服装的单价为60元,等量关系为:七年级服装的总价+八年级服装的总价=5000,根据等量关系式列方程求解即可;
(2)比较两个年级合买服装的总价钱以及按照单价40元买时的总价钱即可得到最省钱的方案.
解:(1)设七年级有![]() 人,则八年级有(92-
人,则八年级有(92-![]() )人.
)人.
根据题意,得![]()
解这个方程,得![]() .
.
八年级人数为:92-52=40(人).
答:七年级有52人,则八年级有40人.
(2)七年级实际参加比赛的人数为:52-10=42,
两个年级联合费用:![]() (元),
(元),
而此时比各自购买节约了:![]() (元);
(元);
若两个年级联合购买91套只需:![]() (元),
(元),
此时又比联合购买91套节约:![]() (元).
(元).
因此,最省钱的购买方案是两校联合购买91套服装,
即比实际人数多买91-(40+42)=9套.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,四边形OBCD是边长为4的正方形,平行于对角线BD的直线l从O出发,沿x轴正方向以每秒1个单位长度的速度运动,运动到直线l与正方形没有交点为止.设直线l扫过正方形OBCD的面积为S,直线l运动的时间为t(秒),下列能反映S与t之间函数关系的图象是( )
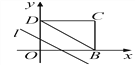
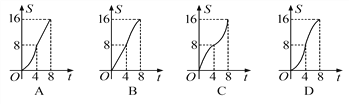
A. A B. B C. C D. D
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABC中,CD⊥AB于点D,BD=9,BC=15,AC=20.
(1)求CD的长;
(2)求AB的长;
(3)判断△ABC的形状.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=
 x+
x+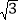 与x轴、y轴分别相交于A,B两点,圆心P的坐标为(1,0),⊙P与y轴相切于点O.若将⊙P沿x轴向左平移,当⊙P与该直线相切时,点P坐标为___.
与x轴、y轴分别相交于A,B两点,圆心P的坐标为(1,0),⊙P与y轴相切于点O.若将⊙P沿x轴向左平移,当⊙P与该直线相切时,点P坐标为___.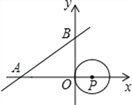
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD 中,G是CD上一点,BG交AD延长线于E,AF=CG,
 .
.(1) 求证:DF=BG;
(2)求
 的度数.
的度数.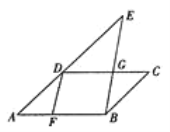

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解学生课余活动情况,某班对参加A组:绘画;B组:书法;C组:舞蹈;D组:乐器;这四个课外兴趣小组的人员分布情况进行抽样调查,并根据收集的数据绘制了如图两幅不完整的统计图,请根据图中提供信息,解答下面的问题:
(1)此次共调查了多少名同学?
(2)将条形统计图补充完整,
(3)计算扇形统计图中书法部分的圆心角的度数;
(4)已知在此次调查中,参加D组的5名学生中有3名女生和2名男生,要从这5名学生中随机抽取2名学生参加市举办的音乐赛,用列表法或画树状图的方法求出抽取的2名学生恰好是1男1女的概率。

-
科目: 来源: 题型:
查看答案和解析>>【题目】身高1.65米的兵兵在建筑物前放风筝,风筝不小心挂在了树上.在如图所示的平面图形中,矩形CDEF代表建筑物,兵兵位于建筑物前点B处,风筝挂在建筑物上方的树枝点G处(点G在FE的延长线上).经测量,兵兵与建筑物的距离BC=5米,建筑物底部宽FC=7米,风筝所在点G与建筑物顶点D及风筝线在手中的点A在同一条直线上,点A距地面的高度AB=1.4米,风筝线与水平线夹角为37°.
(1)求风筝距地面的高度GF;
(2)在建筑物后面有长5米的梯子MN,梯脚M在距墙3米处固定摆放,通过计算说明:若兵兵充分利用梯子和一根米长的竹竿能否触到挂在树上的风筝?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

相关试题

