【题目】如图,△ABC在平面直角坐标系内,顶点的坐标分别为A(﹣1,5),B(﹣4,1),C(﹣1,1)将△ABC绕点A逆时针旋转90°,得到△AB′C′,点B,C的对应点分别为点B′,C′,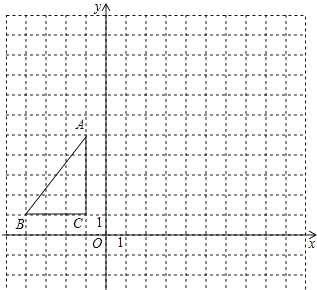
(1)画出△AB′C′;
(2)写出点B′,C′的坐标;
(3)求出在△ABC旋转的过程中,点C经过的路径长.
参考答案:
【答案】
(1)解:△AB′C′如图所示
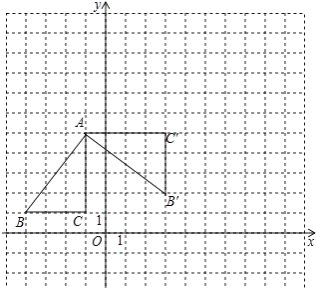
(2)解:点B′的坐标为(3,2),点C′的坐标为(3,5)
(3)解:点C经过的路径为以点A为圆心,AC为半径的圆弧,路径长即为弧长,
∵AC=4,
∴弧长为: ![]() =
= ![]() =2π,
=2π,
即点C经过的路径长为2π.
【解析】(1)根据旋转的性质按要求画出△AB′C′。
(2)观察图形写出点B′,C′的坐标。
(3)根据旋转的现在可知点C经过的路径为以点A为圆心,圆心角为90°,AC为半径的圆弧,根据弧长公式求出弧CC′的长即可
-
科目: 来源: 题型:
查看答案和解析>>【题目】图①是一张∠AOB=45°的纸片折叠后的图形,P、Q分别是边OA、OB上的点,且OP=2cm.将∠AOB沿PQ折叠,点O落在纸片所在平面内的C处(点C在∠AOB的内部或一边上).
(1)当PC∥QB时,OQ= cm.
(2)当折叠后重叠部分为等腰三角形时,画出示意图,写出OQ的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B在反比例函数
 的图象上,且点A、B的横坐标分别为a、2a(a>0),AC⊥x轴,垂足为C,且△AOC的面积为2,
的图象上,且点A、B的横坐标分别为a、2a(a>0),AC⊥x轴,垂足为C,且△AOC的面积为2,
(1)求该反比例函数的解析式;
(2)求△AOB的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的布袋里装有16个只有颜色不同的球,其中红球有x个,白球有2x个,其他均为黄球,现甲从布袋中随机摸出一个球,若是红球则甲同学获胜,甲同学把摸出的球放回并搅匀,由乙同学随机摸出一个球,若为黄球,则乙同学获胜。
(1)当X=3时,谁获胜的可能性大?
(2)当x为何值时,游戏对双方是公平的?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图 , 已知 ∠1+∠2=180,∠3=∠B, 试说明 DE ∥ BC. 下面是部分推导过程,请你在括号内填上推导依据或内容:

证明: ∵∠1+∠2=180( 已知 )
∠1=∠4( )
∴∠2+∠4=180( )
∵EH ∥ AB( )
∴∠B=∠EHC( )
∵∠3=∠B( )
∴∠3=∠EHC( 等量代换 )
∴DE ∥ BC( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是平行四边形,则下列结论中不正确的是( )

A. 当AB=BC时,四边形ABCD是菱形
B. 当AC⊥BD时,四边形ABCD是菱形
C. 当∠ABC=90°时,四边形ABCD是矩形
D. 当AC=BD时,四边形ABCD是正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=
 x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).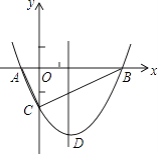
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是抛物线对称轴上的一个动点,当△ACM周长最小时,求点M的坐标及△ACM的最小周长.
相关试题

