搜索
【题目】已知二次函数y＝ax2＋bx＋c满足下表：下列说法：①该函数图像为开口向下的抛物线；②该函数图像的顶点坐标为：(1，3)；③方程ax2＋bx＋c＝－2在2与3之间存在一个根；④A(-2018，m)，B(2019，n)在该二次函数图像上，则m＞n．其中正确的是_______(只需写出序号)．
x | … | -1 | 0 | 1 | 2 | … |
y | … | -5 | 1 | 3 | 1 | … |
参考答案：
【答案】①②③
【解析】
先根据x=0时y=1；x=1时y=3；x=2时，y=1求出a、b、c的值，进而得出二次函数的解析式，再根据二次函数的性质对各小题进行逐一判断即可．
解：由题表可知，x=0时y=1；x=1时y=3；x=2时，y=1，
∴
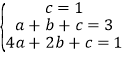，解得：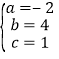
，
∴该二次函数的解析式为：y=﹣2x2+4x+1，
∵a=﹣2＜0，
∴抛物线图象开口向下，故①正确；
∵y=﹣2x2+4x+1=﹣2（x﹣1）2+3，
∴该函数图像的顶点坐标为：(1，3)，故②正确；
∵抛物线的对称轴为直线x=1，
∴当x=3时，y=﹣5，
∴当y=﹣2时，﹣1＜x＜0或2＜x＜3，故③正确；
∵∣﹣2018﹣1∣=2019＞∣2019﹣1∣=2018，
∴m＜n，故④错误.
故答案为：①②③.
-
科目： 来源： 题型：
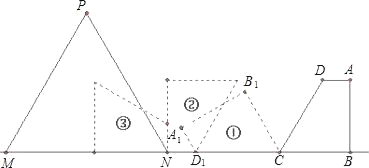
查看答案和解析>>【题目】如图，在直角梯形ABCD中，AD∥BC，AB⊥BC，BC＝5，CD＝6，∠DCB＝60°，等边△PMN（N为固定点）的边长为x，边MN在直线BC上，NC＝8．将直角梯形ABCD绕点C按逆时针方向旋转到①的位置，再绕点D1按逆时针方向旋转到②的位置，如此旋转下去．
（1）将直角梯形按此方法旋转四次，如果等边△PMN的边长为x≥5+3
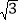，求梯形与等边三角形的重叠部分的面积；（2）将直角梯形按此方法旋转三次，如果梯形与等边三角形的重叠部分的面积是
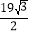，求等边△PMN的边长x的范围．（3）将直角梯形按此方法旋转三次，如果梯形与等边三角形的重叠部分的面积是梯形面积的一半，求等边△PMN的边长x．
-
科目： 来源： 题型：
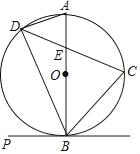
查看答案和解析>>【题目】如图，C、D是以AB为直径的⊙O上的点，
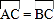，弦CD交AB于点E．（1）当PB是⊙O的切线时，求证：∠PBD=∠DAB；
（2）求证：BC2﹣CE2=CEDE；
（3）已知OA=4，E是半径OA的中点，求线段DE的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，二次函数y＝ax2﹣2ax﹣3a（a＜0）的图象与x轴交于A、B两点（点A在点B的右侧），与y轴的正半轴交于点C，顶点为D．
（1）求顶点D的坐标（用含a的代数式表示）；
（2）若以AD为直径的圆经过点C．
①求抛物线的函数关系式；
②如图2，点E是y轴负半轴上一点，连接BE，将△OBE绕平面内某一点旋转180°，得到△PMN（点P、M、N分别和点O、B、E对应），并且点M、N都在抛物线上，作MF⊥x轴于点F，若线段MF：BF＝1：2，求点M、N的坐标；
③点Q在抛物线的对称轴上，以Q为圆心的圆过A、B两点，并且和直线CD相切，如图3，求点Q的坐标．
-
科目： 来源： 题型：
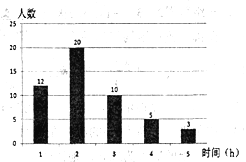
查看答案和解析>>【题目】在创建“书香校园”活动中，为了解学生的读书情况，某校抽样调查了部分同学在一周内的阅读时间，绘制如下统计图．根据图中信息，解答下列问题：
（1）被抽查学生阅读时间的中位数为_______h，众数为________h；平均数为________h：
（2）若该校共有800名学生，请你估算该校一周内阅读时间不少于3h的学生人数．
-
科目： 来源： 题型：
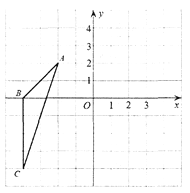
查看答案和解析>>【题目】如图，在平面直角坐标系中，△ABC的顶点坐标分别为A(－2，2)，B(－4，0)，C(－4；－4)，
（1）在y轴右侧，以O为位似中心，画出△A'B'C′，使它与△ABC的相似比为1:2；
（2）根据(1)的作图，sin∠A'C'B′＝__________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】下图为水平放置于桌面上的台灯的示意图，已知灯臂AB＝18cm，灯罩BC＝30cm，∠BAM＝60°，∠ABC＝90°，求点C到桌面的距离CD(精确到0．1cm)．参考数据：
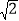≈1.41，
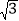≈1.73．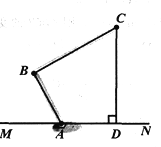
相关试题
