搜索
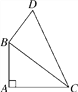
【题目】如图所示，在四边形ABDC中，∠A＝90°，AB＝9，AC＝12，BD＝8，CD＝17.
(1)连接BC，求BC的长；
(2)求四边形ABDC的面积．
参考答案：
【答案】(1)15；(2) 114.
【解析】(1)、根据Rt△ABC的勾股定理得出BC的长度；(2)、根据三角形三边关系得出△BCD为直角三角形，然后根据S四边形ABDC＝SRt△ABC＋SRt△BCD得出答案．
(1)∵∠A＝90°，∴△ABC是直角三角形．
在Rt△ABC中，AB＝9，AC＝12， ∴BC＝
＝15．
(2)∵BD＝8，CD＝17，由(1)可知BC＝15， ∴BC2＋BD2＝152＋82＝172＝CD2，
∴△BCD是直角三角形，且∠CBD＝90°，
∴S四边形ABDC＝SRt△ABC＋SRt△BCD＝
．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，AB＝10，AC＝2
，BC边上的高AD＝6，则另一边BC等于_______．【答案】10或6
【解析】试题解析：根据题意画出图形，如图所示，
如图1所示，AB=10，AC=2
，AD=6，在Rt△ABD和Rt△ACD中，
根据勾股定理得：BD=
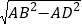=8，CD=
=2，此时BC=BD+CD=8+2=10；
如图2所示，AB=10，AC=2
，AD=6，在Rt△ABD和Rt△ACD中，
根据勾股定理得：BD=
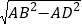=8，CD==2，此时BC=BD-CD=8-2=6，
则BC的长为6或10．
【题型】填空题
【结束】
12【题目】在平面直角坐标系中，已知一次函数y=2x+1的图象经过P1（x1，y1）、P2（x2，y2）两点，若x1＜x2，则y1 ______ y2．（填“＞”“＜”或“=”）
-
科目： 来源： 题型：
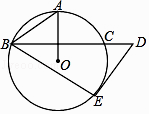
查看答案和解析>>【题目】如图，OA是⊙O的半径，BC是⊙O的弦，且BC⊥OA，过BC的延长线上一点D作⊙O的切线DE，切点为E，连接AB，BE，若∠BDE=52°，则∠ABE的度数是（ ）
A.52°
B.58°
C.60°
D.64° -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，矩形ABCD中，AB=8,AD=5，点E
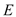为DC边上一个动点，把△ADE沿AE折叠，点D的对应点D’落在矩形ABCD的对称轴上时，DE的长为____________.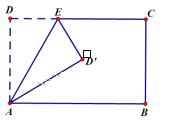
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，三角形DEF是三角形ABC经过某种变换得到的图形，点A与点D，点B与点E，点C与点F分别是对应点，观察点与点的坐标之间的关系，解答下列问题：
(1)分别写出点A与点D，点B与点E，点C与点F的坐标，并说说对应点的坐标有哪些特征；
(2)若点P(a＋3，4－b)与点Q(2a，2b－3)也是通过上述变换得到的对应点，求a，b的值.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCO在平面直角坐标系中，且A(1，2)，B(5，4)，C(6，0)，O(0，0)．
(1)求四边形ABCO的面积；
(2)将四边形ABCO四个顶点的横坐标都减去3，同时纵坐标都减去2，画出得到的四边形A′B′C′O′，你能从中得到什么结论？
(3)直接写出四边形A′B′C′O′的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形ABCD和正方形A1B1C1D1的对角线(正方形相对顶点之间所连的线段)BD，B1D1都在x轴上，O，O1分别为正方形ABCD和正方形A1B1C1D1的中心(正方形对角线的交点称为正方形的中心)，O为平面直角坐标系的原点．OD＝3，O1D1＝2.
(1)如果O1在x轴上平移时，正方形A1B1C1D1也随之平移，其形状、大小没有改变，当中心O1在x轴上平移到两个正方形只有一个公共点时，求此时正方形A1B1C1D1各顶点的坐标；
(2)如果O在x轴上平移时，正方形ABCD也随之平移，其形状、大小没有改变，当中心O在x轴上平移到两个正方形公共部分的面积为2个平方单位时，求此时正方形ABCD各顶点的坐标．
相关试题
