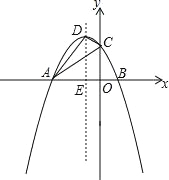
【题目】如图,抛物线y=﹣x2+bx+c与x轴分别交于点A(﹣3,0)和点B,与y轴交于点C(0,3),顶点为点D,对称轴DE交x轴于点E,连接AD,AC,DC.
(1)求抛物线的函数表达式.
(2)判断△ADC的形状,并说明理由.
(3)对称轴DE上是否存在点P,使点P到直线AD的距离与到x轴的距离相等?若存在,求出点P的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)抛物线解析式为y=﹣x2﹣2x+3;(2)
【解析】
试题分析:(1)用待定系数法求出抛物线解析式;
(2)先确定出抛物线的顶点坐标,从而求出AD,AC,CD,用勾股定理的逆定理判断即可;
(3)先求出∠ADE的正弦值,再分点P在∠DAB的平分线和∠DAB的外角的平分线两种情况用PM=PE建立方程求解即可.
试题解析:(1)∵点A(﹣3,0),C(0,3)在抛物线y=﹣x2+bx+c的图象上,
∴![]() ,∴
,∴![]() ,
,
∴抛物线解析式为y=﹣x2﹣2x+3,
(2)由(1)得抛物线解析式为y=﹣x2﹣2x+3=﹣(x+1)2+4,
∴抛物线的顶点D(﹣1,4),∵C(0,3),A(﹣3,0),
∴AD=2![]() ,AC=3
,AC=3![]() ,CD=
,CD=![]() ,∴AD2=AC2+CD2,
,∴AD2=AC2+CD2,
∴△ADC是直角三角形;
(3)存在,
理由:∵抛物线解析式为y=﹣x2﹣2x+3=﹣(x+1)2+4,
∴E(﹣1,0),
∵A(﹣3,0),D(﹣1,4),
∴AE=2,DE=4,AD=2![]() ,
,
在Rt△ADE中,sin∠ADE=![]() =
=![]() ,
,
设P(﹣1,p),
∵点P到直线AD的距离与到x轴的距离相等
①当点P在∠DAB的角平分线时,
如图1,
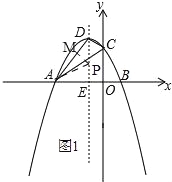
过点P作PM⊥AD,
∴PM=PD×sin∠ADE=![]() (4﹣p),PE=p,
(4﹣p),PE=p,
∵PM=PE,
∴![]() (4﹣p)=p,
(4﹣p)=p,
∴p=![]() ﹣1,
﹣1,
∴P(﹣1,![]() ﹣1),
﹣1),
②当点P在∠DAB的外角的平分线时,
如图2,
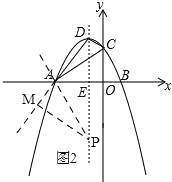
过点P作PM⊥AD,∴PM=PD×sin∠ADE=![]() (4﹣p),PE=﹣p,
(4﹣p),PE=﹣p,
∴![]() (4﹣p)=﹣p,∴p=﹣
(4﹣p)=﹣p,∴p=﹣![]() ﹣1,∴P(﹣1,﹣
﹣1,∴P(﹣1,﹣![]() ﹣1),
﹣1),
综上所述,存在点P到AD的距离与到x轴的距离相等,点P(﹣1,![]() ﹣1)或(﹣1,﹣
﹣1)或(﹣1,﹣![]() ﹣1).
﹣1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】六十四名学生外出参加竞赛,共租车10辆,其中大车每辆可坐8人,小车每辆可坐4人,则大、小车各租多少辆?
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)﹣40﹣28﹣(﹣19)+(﹣24)
(2)﹣82+3×(﹣2)2+6÷(﹣ )2
)2
(3)﹣24×(﹣ +
+  ﹣
﹣  )
)
(4)﹣12016﹣(1﹣0.5)× ×[3﹣(﹣3)2]
×[3﹣(﹣3)2]
(5)x+7x﹣5x
(6)﹣4x2y+3xy2﹣9x2y﹣5xy2
(7)4(2x2﹣y2)﹣5(3y2﹣x2) -
科目: 来源: 题型:
查看答案和解析>>【题目】-3的相反数是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式:
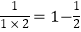 ,
, 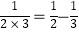 ,
, 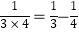 ,
,
将以上三个等式两边分别相加得: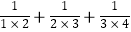 =1﹣
=1﹣ 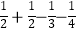 =1﹣
=1﹣  =
=  .
.
(1)猜想并写出: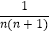 = .
= .
(2)直接写出下列各式的计算结果:
①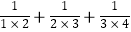 +…+
+…+ 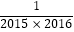 =;
=;
②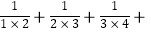 …+
…+ 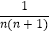 =;
=;
(3)探究并计算: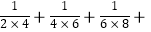 …+
…+ 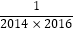 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a、b互为相反数,c、d互为倒数,并且x的绝对值等于2.试求:x2﹣(a+b+cd)+(a+b)2016+(﹣cd)2016的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式计算正确的是( )
A.2a2+3a2=5a4
B.(﹣2ab)3=﹣6ab3
C.(3a+b)(3a﹣b)=9a2﹣b2
D.a3(﹣2a)=﹣2a3
相关试题

