【题目】如图,AD是△ABC的中线,tanB=![]() , cosC=
, cosC=![]() , AC=
, AC=![]() . 求:
. 求:
(1)BC的长;
(2)sin∠ADC的值.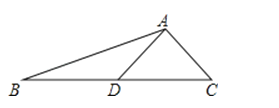
参考答案:
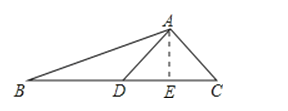
【答案】解:(1)过点A作AE⊥BC于点E,
∵cosC=![]() ,
,
∴∠C=45°,
在Rt△ACE中,CE=ACcosC=1,
∴AE=CE=1,
在Rt△ABE中,tanB=![]() ,即
,即![]() =
=![]() ,
,
∴BE=3AE=3,
∴BC=BE+CE=4;
(2)∵AD是△ABC的中线,
∴CD=![]() BC=2,
BC=2,
∴DE=CD﹣CE=1,
∵AE⊥BC,DE=AE,
∴∠ADC=45°,
∴sin∠ADC=![]() .
.
【解析】(1)过点A作AE⊥BC于点E,根据cosC=![]() , 求出∠C=45°,求出AE=CE=1,根据tanB=
, 求出∠C=45°,求出AE=CE=1,根据tanB=![]() , 求出BE的长即可;
, 求出BE的长即可;
(2)根据AD是△ABC的中线,求出BD的长,得到DE的长,得到答案.
【考点精析】解答此题的关键在于理解解直角三角形的相关知识,掌握解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:∠MON=30°,点A1、A2、A3在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A6B6A7的边长为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】定义新运算:对于任意有理数a,b,都有a*b=b(a﹣b)﹣b,等式右边是通常的加法、减法及乘法运算,例如:2*5=5×(2﹣5)﹣5=﹣20.
(1)求2*(﹣5)的值;
(2)若x*(﹣2)的值大于﹣6且小于9,求x的取值范围,并在如图所示的所画的数轴上表示出来.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:关于x、y的方程组
 的解为非负数.
的解为非负数.(1)求a的取值范围;
(2)化简|2a+4|﹣|a﹣1|;
(3)在a的取值范围内,a为何整数时,使得2ax+3x<2a+3解集为x>1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,请按照图中所标注的数据计算图中实线所围成的图形的面积S=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)求出△ABC的面积;
(2)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(3)写出点A1,B1,C1的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】钓鱼岛是我国的神圣领土,中国人民维护国家领土完整的决心是坚定的,多年来,我国的海监、渔政等执法船定期开赴钓鱼岛巡视.某日,我海监船(A处)测得钓鱼岛(B处)距离为20海里,海监船继续向东航行,在C处测得钓鱼岛在北偏东45°的方向上,距离为10
 海里,求AC的距离.(结果保留根号)
海里,求AC的距离.(结果保留根号)
相关试题

