【题目】已知甲、乙两地相距90km,A,B两人沿同一公路从甲地出发到乙地,A骑摩托车,B骑电动车,图中DE,OC分别表示A,B离开甲地的路程s(km)与时间t(h)的函数关系的图象,根据图象解答下列问题. 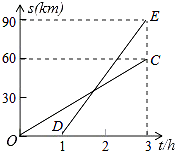
(1)A比B后出发几个小时?B的速度是多少?
(2)在B出发后几小时,两人相遇?
参考答案:
【答案】
(1)解:由图可知,A比B后出发1小时;
B的速度:60÷3=20(km/h)
(2)解:由图可知点D(1,0),C(3,60),E(3,90),
设OC的解析式为s=kt,
则3k=60,
解得k=20,
所以,s=20t,
设DE的解析式为s=mt+n,
则 ![]() ,
,
解得 ![]() ,
,
所以,s=45t﹣45,
由题意得 ![]() ,
,
解得  ,
,
所以,B出发 ![]() 小时后两人相遇.
小时后两人相遇.
【解析】(1)根据CO与DE可得出A比B后出发1小时;由点C的坐标为(3,60)可求出B的速度;(2)利用待定系数法求出OC、DE的解析式,联立两函数解析式建立方程求解即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为n的正方形OABC的边OA,OC在坐标轴上,点A1 , A2 , …,An﹣1为OA的n等分点,点B1 , B2 , …,Bn﹣1为CB的n等分点,连结A1B1 , A2B2 , …,An﹣1Bn﹣1 , 分别交曲线y=
 (x>0)于点C1 , C2 , …,Cn﹣1 . 若C15B15=16C15A15 , 则n的值为 . (n为正整数)
(x>0)于点C1 , C2 , …,Cn﹣1 . 若C15B15=16C15A15 , 则n的值为 . (n为正整数) 
-
科目: 来源: 题型:
查看答案和解析>>【题目】把标准纸一次又一次对开,可以得到均相似的“开纸”.现在我们在长为2
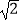 、宽为1的矩形纸片中,画两个小矩形,使这两个小矩形的每条边都与原矩形纸的边平行,或小矩形的边在原矩形的边上,且每个小矩形均与原矩形纸相似,然后将它们剪下,则所剪得的两个小矩形纸片周长之和的最大值是 .
、宽为1的矩形纸片中,画两个小矩形,使这两个小矩形的每条边都与原矩形纸的边平行,或小矩形的边在原矩形的边上,且每个小矩形均与原矩形纸相似,然后将它们剪下,则所剪得的两个小矩形纸片周长之和的最大值是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题
(1)计算: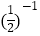 ﹣4sin45°﹣
﹣4sin45°﹣ 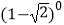 +
+  .
.
(2)先化简,再求值:a(a﹣3b)+(a+b)2﹣a(a﹣b),其中a=1,b=﹣ .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某校七,八年级学生的睡眠情况,随机抽取了该校七,八年级部分学生进行调查,已知抽取七年级与八年级的学生人数相同,利用抽样所得的数据绘制如下统计图表.

睡眠情况分组表(单位:时)组别
睡眠时间x
A
x≤7.5
B
7.5≤x≤8.5
C
8.5≤x≤9.5
D
9.5≤x≤10.5
E
x≥10.5
根据图表提供的信息,回答下列问题:
(1)求统计图中的a;
(2)抽取的样本中,八年级学生睡眠时间在C组的有多少人?
(3)已知该校七年级学生有755人,八年级学生有785人,如果睡眠时间x(时)满足:7.5≤x≤9.5,称睡眠时间合格,试估计该校七、八年级学生中睡眠时间合格的共有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】课本中有一道作业题: 有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.问加工成的正方形零件的边长是多少mm?
小颖解得此题的答案为48mm,小颖善于反思,她又提出了如下的问题.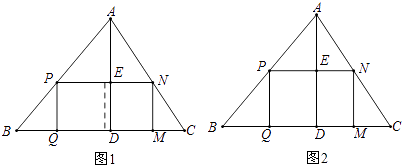
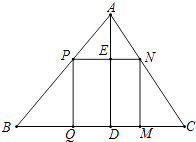
(1)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1,此时,这个矩形零件的两条边长又分别为多少mm?请你计算.
(2)如果原题中所要加工的零件只是一个矩形,如图2,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长. -
科目: 来源: 题型:
查看答案和解析>>【题目】九(1)班同学在上学期的社会实践活动中,对学校旁边的山坡护墙和旗杆进行了测量.

(1)如图1,第一小组用一根木条CD斜靠在护墙上,使得DB与CB的长度相等,如果测量得到∠CDB=38°,求护墙与地面的倾斜角α的度数.
(2)如图2,第二小组用皮尺量的EF为16米(E为护墙上的端点),EF的中点离地面FB的高度为1.9米,请你求出E点离地面FB的高度.
(3)如图3,第三小组利用第一、第二小组的结果,来测量护墙上旗杆的高度,在点P测得旗杆顶端A的仰角为45°,向前走4米到达Q点,测得A的仰角为60°,求旗杆AE的高度(精确到0.1米).
备用数据:tan60°=1.732,tan30°=0.577, =1.732,
=1.732, 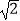 =1.414.
=1.414.
相关试题

