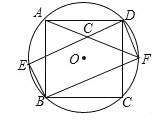
【题目】(2016山东潍坊第21题)正方形ABCD内接于⊙O,如图所示,在劣弧![]() 上取一点E,连接DE、BE,过点D作DF∥BE交⊙O于点F,连接BF、AF,且AF与DE相交于点G,求证:
上取一点E,连接DE、BE,过点D作DF∥BE交⊙O于点F,连接BF、AF,且AF与DE相交于点G,求证:
(1)四边形EBFD是矩形;
(2)DG=BE.
参考答案:
【答案】(1)详见解析;(2)详见解析.
【解析】
试题分析:(1)根据正方形的性质、圆周角定理及平行线的性质易证∠BED=∠BAD=90°,∠BFD=∠BCD=90°,∠EDF=90°,即可判定四边形EBFD是矩形;(2)根据正方形的性质可得![]() 的度数是90°,进而得出BE=DF,则BE=DG.
的度数是90°,进而得出BE=DF,则BE=DG.
试题解析:(1)∵正方形ABCD内接于⊙O,
∴∠BED=∠BAD=90°,∠BFD=∠BCD=90°,
又∵DF∥BE,
∴∠EDF+∠BED=180°,
∴∠EDF=90°,
∴四边形EBFD是矩形;
(2))∵正方形ABCD内接于⊙O,
∴![]() 的度数是90°,
的度数是90°,
∴∠AFD=45°,
又∵∠GDF=90°,
∴∠DGF=∠DFC=45°,
∴DG=DF,
又∵在矩形EBFD中,BE=DF,
∴BE=DG.
-
科目: 来源: 题型:
查看答案和解析>>【题目】.如图1,在矩形ABCD中,BC>AB,∠BAD的平分线AF与BD、BC分别交于点E、F,点O是BD的中点,直线OK∥AF,交AD于点K,交BC于点G.
(1)求证:①△DOK≌△BOG;②AB+AK=BG;
(2)若KD=KG,BC=4﹣.
①求KD的长度;
②如图2,点P是线段KD上的动点(不与点D、K重合),PM∥DG交KG于点M,PN∥KG交DG于点N,设PD=m,当S△PMN=
 时,求m的值.
时,求m的值.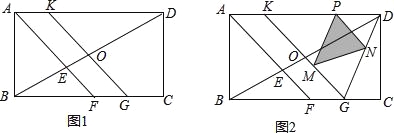
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列性质中,菱形具有而矩形不一定具有的性质是( ).
A.对边平行且相等B.对角线互相平分
C.内角和等于外角和D.每一条对角线所在直线都是它的对称轴
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列方程是一元二次方程的是( )
A. ax2+bx+c=0B. 3x2﹣2x=3(x2﹣2)
C. x3﹣2x﹣4=0D. (x﹣1)2+1=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】若等腰三角形的底角为54°,则顶角为( )
A. 108° B. 72° C. 54° D. 36°
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.2a+3b=5ab
B.a2a3=a5
C.(2a)3=6a3
D.a6+a3=a9 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的有( )
①等腰三角形的两腰相等;②等腰三角形的两底角相等;③等腰三角形底边上的中线与底边上的高相等;④等腰三角形是轴对称图形.
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

