Question

【题目】阅读下列材料：

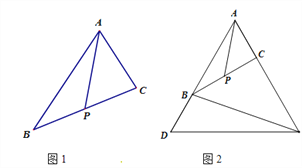
问题：如图1，在△中，点为的中点，求证： ＜小明提供了他研究这个问题的思路：从点为的中点出发，可以构造以、为邻边的平行四边形，结合平行四边形的性质以及三角形两边之和大于第三边的性质便可解决这个问题.请结合小明研究问题的思路，解决下列问题：

（1）完成上面问题的解答；

（2）如果在图1中，∠=60°，延长到，使得，延长到，使得，连结，如图2. 请猜想线段与线段之间的数量关系.并加以证明.

Answer 1

【答案】（1）证明见解析；（2）BE=2AP，证明见解析

【解析】试题分析：（1）可通过构建平行四边形求解；延长AP至H，使PH=AP；则AH、BC互相平分，四边形ABHC是平行四边形；在△ACH中，由三角形三边关系定理知：AH<AC+CH，而HC=AB，AH=2AP，等量代换后即可证得所求的结论；

（2）可按照（1）题的思路求解；过B作AE的平行线，交DE于H，连接AH、CH；易知AD=AE，若∠BAC=60°，则△ADE是等边三角形，易证得△DBH也是等边三角形，此时DB=BH=AC，则四边形ABHC的一组对边平行且相等，则四边形ABHC是平行四边形；由此可证得P是平行四边形ABHC对角线的交点，且AH=2AP；下面可通过证△DBE≌△DHA得出AH=DE，从而得出DE=2AP的结论；

试题解析：

(1)证明：延长AP至H，使得PH=AP，连接BH、HC，PH；

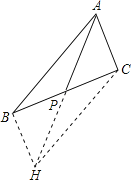
∵BP=PC；

∴四边形ABHC是平行四边形；

∴AB=HC；

在△ACH中，AH<HC+AC；

∴2AP<AB+AC；

即AP< (AB+AC)

(2) BE=2AP.

证明：过B作BH∥AE交DE于H，连接CH、AH；

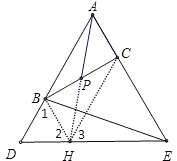
∴∠1=∠BAC=60°；

∵DB=AC，AB=CE，

∴AD=AE,

∴△AED是等边三角形，

∴∠D=∠1=∠2=∠AED=60°；

∴△BDH是等边三角形；

∴BD=DH=BH=AC；

∴四边形ABHC是平行四边形；

∵点P是BC的中点，

∴点P是四边形ABHC对角线AH、BC的交点，

∴点A，P，H共线，

∴AH=2AP；

在△ADH和△EDB中, ；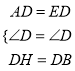

∴△ADH≌△EDB；

∴AH=BE=2AP；