【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:
①b2>4ac;
②abc>0;
③2a﹣b=0;
④8a+c<0;
⑤9a+3b+c<0,
其中结论正确有( )个。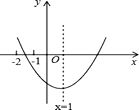
A.2个
B.3个
C.4个
D.5个
参考答案:
【答案】B
【解析】图象与x轴有两个交点,则 ![]() -4ac>0,则
-4ac>0,则 ![]() >4ac,∴①正确;根据图形可得:a>0,b<0,c<0,则abc>0,∴②正确;根据对称轴为x=1,即-
>4ac,∴①正确;根据图形可得:a>0,b<0,c<0,则abc>0,∴②正确;根据对称轴为x=1,即- ![]() =1,则-b=2a,则2a+b=0,∴③错误;当x=-2时,y>0,即4a-2b+c>0,根据③可得:-b=2a,则4a+4a+c>0,即8a+c>0,∴④错误;根据图象可得:当x=3和x=-1时y的值相等,当x=-1时,y>0,所以当x=3时,y>0,即9a+3b+c>0,∴⑤正确.∴①、②、⑤正确.
=1,则-b=2a,则2a+b=0,∴③错误;当x=-2时,y>0,即4a-2b+c>0,根据③可得:-b=2a,则4a+4a+c>0,即8a+c>0,∴④错误;根据图象可得:当x=3和x=-1时y的值相等,当x=-1时,y>0,所以当x=3时,y>0,即9a+3b+c>0,∴⑤正确.∴①、②、⑤正确.
答案:B
【考点精析】利用二次函数图象以及系数a、b、c的关系对题目进行判断即可得到答案,需要熟知二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c的图象经过(-1,0)(0,3),下列结论中错误的是( )
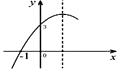
A.abc<0
B.9a+3b+c=0
C.a-b=-3
D.4ac﹣b2<0 -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题8分) 已知,如图,AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=DC.
(1)求证:BE=DF;
(2)若AB=5,AD=3,求AE的长;
(3)若△ABC的面积是23,△ADC面积是18,则△BEC的面积等于 .
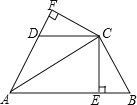
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=3x2 , y=-3x2 , y=
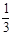 x2+3共有的性质是( )
x2+3共有的性质是( )
A.开口向上
B.对称轴是y轴
C.都有最高点
D.y随x值的增大而增大 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )

A.2
B.2
C.2
D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB为⊙O的直径AC、AD为⊙O的弦,若AB=2AC=
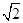 AD,则∠DBC的度数为 .
AD,则∠DBC的度数为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=6,AD=8,P是AD上的动点,PE⊥AC,PF⊥BD于F,求PE+PF的值.

相关试题

