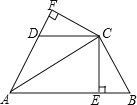
【题目】(本题8分) 已知,如图,AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=DC.
(1)求证:BE=DF;
(2)若AB=5,AD=3,求AE的长;
(3)若△ABC的面积是23,△ADC面积是18,则△BEC的面积等于 .
参考答案:
【答案】(1)证明见解析;(2)4;(3)2.5.
【解析】试题分析:(1)根据HL证明Rt△BCE与Rt△DCF全等,再利用全等三角形的性质解答即可;
(2)根据全等三角形的性质解答即可;
(3)利用三角形的面积公式解答即可.
试题解析:解:(1)相等,∵AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,∴CE=CF,在Rt△BCE与Rt△DCF中,∵CE=CF,BC=CD,∴Rt△BCE≌Rt△DCF(HL),∴BE=DF;
(2)∵Rt△BCE≌Rt△DCF,∴DF=EB,CE=CF,CE⊥AB于E,CF⊥AD于F,在Rt△ACE与Rt△ACF中,∵CE=CF,AC=AC,∴Rt△ACERt△ACF(HL),∴AF=AE,∵DF=1,AD=3,∴AB=AF+BE=AD+DF+BE=5;
(3)∵Rt△BCE≌Rt△DCF,∵△ABC的面积是23,△ADC面积是18,∴△BEC的面积=![]() ×(23-18)=2.5.
×(23-18)=2.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果5x|m|y2﹣(m﹣2)xy﹣3x是关于x、y的四次三项式,则m= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B在小正方形的顶点上.
(1)在直线l上找一点C,使它到A,B两点的距离相等;
(2)在(1)的基础上画出△ABC关于直线l成轴对称的△A′B′C′;
(3)在直线l上找一点P(在答题纸上图中标出),使PA+PB的长最短,这个最短长度的平方值是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】(2x2y﹣4xy2)﹣(﹣3xy2+x2y),其中x=﹣1,y=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某产品的成本两年降低了75%,平均每年递降( )
A.50%
B.25%
C.37.5%
D.以上答案都不对 -
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一道题:“计算(2x3﹣3x2y﹣2xy2)﹣(x3﹣2xy2+y3)+(﹣x3+3x2y﹣y3)的值,其中
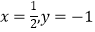 ”.甲同学把“
”.甲同学把“ 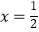 ”错抄成“
”错抄成“ 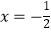 ”,但他计算的结果也是正确的,试说明理由,并求出这个结果.
”,但他计算的结果也是正确的,试说明理由,并求出这个结果. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为1的正方形ABCD绕点A逆时针旋转45度后得到正方形AB′C′D′,边B′C′与DC交于点O,则四边形AB′OD的周长是( )

A.2

B.3
C.

D.1+

相关试题

