搜索
【题目】如图，△ABC和△DEB都是等边三角形，点A、D、B在同一直线上，如图1．
（1）求证：DC=AE；
（2）若BM⊥CD，BN⊥AE，垂足分别为M、N，如图2，求证：△BMN是等边三角形．
参考答案：
【答案】（1）见解析；（2）见解析
【解析】
（1）根据等边三角形的性质证明△CBD≌△ABE即可解决问题；
（2）根据△CBD≌△ABE可得∠BCM=∠BAN，进而证明△CMB≌△ANB，然后根据全等三角形的性质及等边三角形的判定定理得出结论．
证明：（1）∵△ABC和△DEB都是等边三角形，
∴CB=AB，∠CBA=∠DBE=60°，DB=BE，
∴△CBD≌△ABE（SAS），
∴DC=AE；
（2）∵BM⊥CD，BN⊥AE，
∴∠CMB=∠ANB=90°，
∵△CBD≌△ABE，
∴∠BCM=∠BAN，
∵CB=AB，
∴△CMB≌△ANB（AAS），
∴BM=BN，∠CBM=∠ABN，
∴∠ABN+∠ABM=∠CBM+∠ABM=∠CBA=60°，即∠MBN=60°，
∴△BMN是等边三角形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】四边形ABCD内接于⊙O，点E为AD上一点，连接AC，CB，∠B=∠AEC．
（1）如图1，求证：CE=CD；
（2）如图2，若∠B+∠CAE=120°，∠ACD=2∠BAC，求∠BAD的度数；
（3）如图3，在（2）的条件下，延长CE交⊙O于点G，若tan∠BAC=
，EG=2，求AE的长．
【答案】（1）见解析；（2）60°；（3）7.
【解析】试题分析：(1)利用圆的内接四边形定理得到∠CED=∠CDE.
(2) 作CH⊥DE于H, 设∠ECH=α，由（1）CE=CD，用α表示∠CAE，∠BAC，而∠BAD=∠BAC+∠CAE.（3）连接AG，作GN⊥AC，AM⊥EG，先证明∠CAG=∠BAC，设NG=5
m，可得AN=11m，利用直角
AGM, 
AEM，勾股定理可以算出m的值并求出AE长.试题解析：
（1）解：证明：∵四边形ABCD内接于⊙O.
∴∠B+∠D=180°，
∵∠B=∠AEC，
∴∠AEC+∠D=180°，
∵∠AEC+∠CED=180°，
∴∠D=∠CED，
∴CE=CD．
（2）解：作CH⊥DE于H．
设∠ECH=α，由（1）CE=CD，
∴∠ECD=2α，
∵∠B=∠AEC，∠B+∠CAE=120°，
∴∠CAE+∠AEC=120°，
∴∠ACE=180°﹣∠AEC﹣∠ACE=60°，
∴∠CAE=90°﹣∠ACH=90°﹣（60°+α）=30°﹣α，
∠ACD=∠ACH+∠HCD=60°+2α，
∵∠ACD=2∠BAC，
∴∠BAC=30°+α，
∴∠BAD=∠BAC+∠CAE=30°+α+30°﹣α=60°．
（3）解：连接AG，作GN⊥AC，AM⊥EG，
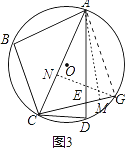
∵∠CED=∠AEG，∠CDE=∠AGE，∠CED=∠CDE，
∴∠AEG=∠AGE，
∴AE=AG，
∴EM=MG=
EG=1，∴∠EAG=∠ECD=2α，
∴∠CAG=∠CAD+∠DAG=30°﹣α+2α=∠BAC，
∵tan∠BAC=
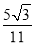，∴设NG=5
m，可得AN=11m，AG=
=14m，∵∠ACG=60°，
∴CN=5m，AM=8
m，MG=
=2m=1，∴m=
，∴CE=CD=CG﹣EG=10m﹣2=3，
∴AE=
=
=7．【题型】解答题
【结束】
27【题目】二次函数y=（x﹣1）2+k分别与x轴、y轴交于A、B、C三点，点A在点B的左侧，直线y=﹣
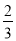x+2经过点B，且与y轴交于点D． （1）如图1，求k的值；
（2）如图2，在第一象限的抛物线上有一动点P，连接AP，过P作PE⊥x轴于点E，过E作EF⊥AP于点F，过点D作平行于x轴的直线分别与直线FE、PE交于点G、H，设点P的横坐标为t，线段GH的长为d，求d与t的函数关系式，并直接写出t的取值范围；
（3）在（2）的条件下，过点G作平行于y轴的直线分别交AP、x轴和抛物线于点M、T和N，tan∠MEA=
，点K为第四象限抛物线上一点，且在对称轴左侧，连接KA，在射线KA上取一点R，连接RM，过点K作KQ⊥AK交PE的延长线于Q，连接AQ、HK，若∠RAE﹣∠RMA=45°，△AKQ与△HKQ的面积相等，求点R的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】射击队为从甲、乙两名运动员中选拔一人参加比赛，对他们进行了六次测试，测试成绩如下表（单位：环）：
第一次
第二次
第三次
第四次
第五次
第六次
平均成绩
中位数
甲
10
8
9
8
10
9
9
①
乙
10
7
10
10
9
8
②
9.5
（1）完成表中填空① ；② ；
（2）请计算甲六次测试成绩的方差；
（3）若乙六次测试成绩方差为
，你认为推荐谁参加比赛更合适，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知
、
是关于
的方程
的两个不相等的实数根.(1)求实数
的取值范围;(2)已知等腰
的一边长为7，若
、
恰好是
另外两边长，求这个三角形的周长. -
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，△ABC中，AC=BC，以BC为直径的⊙O交AB于点D，过点D作DE⊥AC于点E，交BC的延长线于点F．
求证：
（1）AD=BD；
（2）DF是⊙O的切线．
-
科目： 来源： 题型：
查看答案和解析>>【题目】(1) 定义：直角三角形两直角边的平方和等于斜边的平方．如：直角三角形的直角边分别为3、4，则斜边的平方=32+42=25.已知：Rt△ABC中，∠C=90°，AC=8，AB=10,直接写出BC2=__________________．
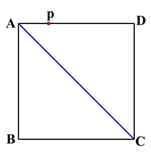
（2）应用：已知正方形ABCD的边长为4，点P为AD边上的一点，AP=
,请利用“两点之间线段最短”这一原理，在线段AC上画出一点M，使MP+MD最小，并直接写出最小值的平方为_____________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知四边形ABCD是正方形，点B，C分别在直线
和
上，点A，D是x轴上两点.
（1）若此正方形边长为2，k=_______.
（2）若此正方形边长为a，k的值是否会发生变化？若不会发生变化，请说明理由；若会发生变化，求出a的值.
相关试题
