【题目】某兴趣小组开展课外活动.如图,A,B两地相距12米,小明从点A出发沿AB方向匀速前进,2秒后到达点D,此时他(CD)在某一灯光下的影长为AD,继续按原速行走2秒到达点F,此时他在同一灯光下的影子仍落在其身后,并测得这个影长为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点H,此时他(GH)在同一灯光下的影长为BH(点C,E,G在一条直线上).
(1)请在图中画出光源O点的位置,并画出他位于点F时在这个灯光下的影长FM(不写画法);
(2)求小明原来的速度.
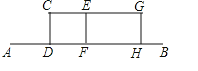
参考答案:
【答案】(1)作图见试题解析;(2)1.5m/s.
【解析】
试题分析:(1)利用中心投影的定义作图;
(2)设小明原来的速度为xm/s,则CE=2xm,AM=(4x﹣1.2)m,EG=3xm,BM=13.2﹣4x,由△OCE∽△OAM,△OEG∽△OMB,得到![]() ,即代入解方程即可.
,即代入解方程即可.
试题解析:(1)如图,
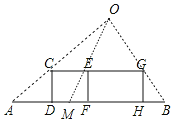
(2)设小明原来的速度为xm/s,则CE=2xm,AM=AF﹣MF=(4x﹣1.2)m,EG=2×1.5x=3xm,BM=AB﹣AM=12﹣(4x﹣1.2)=13.2﹣4x,∵点C,E,G在一条直线上,CG∥AB,∴△OCE∽△OAM,△OEG∽△OMB,∴![]() ,
,![]() ,∴
,∴![]() ,即
,即![]() ,解得x=1.5,经检验x=1.5为方程的解,∴小明原来的速度为1.5m/s.
,解得x=1.5,经检验x=1.5为方程的解,∴小明原来的速度为1.5m/s.
答:小明原来的速度为1.5m/s.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组:
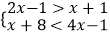 ,并把解集表示在数轴上.
,并把解集表示在数轴上. -
科目: 来源: 题型:
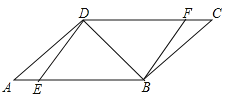
查看答案和解析>>【题目】如图,在ABCD中,点E,F分别在AB,DC上,且ED⊥DB,FB⊥BD.
(1)求证:△AED≌△CFB;
(2)若∠A=30°,∠DEB=45°,求证:DA=DF.
-
科目: 来源: 题型:
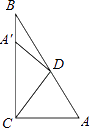
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,∠A=55°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB=( )
A.40°
B.30°
C.20°
D.10° -
科目: 来源: 题型:
查看答案和解析>>【题目】【阅读材料,获取新知】
善于思考的小军在解方程组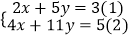 时,采用了一种“整体代换法”的解法.
时,采用了一种“整体代换法”的解法.
解:将方程(2)变形:4x+10y+y=5即2(2x+5y)+y=5(3)
把方程(1)代入(3)得:2×3+y=5
∴y=﹣1.
把y=﹣1,代入(1)得x=4
∴方程组的解为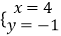
【利用新知,解答问题】
请你利用小军的“整体代换法”解决一下问题:
(1)解方程组:
①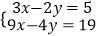 ②
② 
(2)已知x,y满足方程组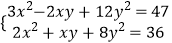 ,则x2+4y2与xy的值分别为、 .
,则x2+4y2与xy的值分别为、 . -
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
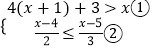 ,并把解集在数轴上表示出来,再求出符合条件的正整数解.
,并把解集在数轴上表示出来,再求出符合条件的正整数解. -
科目: 来源: 题型:
查看答案和解析>>【题目】综合题。
(1)因式分解:a3﹣2a2+a;
(2)因式分解:(3x+y)2﹣(x﹣3y)2;
(3)解方程: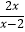 =1﹣
=1﹣ 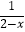 .
.
相关试题

