【题目】如图,矩形ABCD中,AB=4,AD=3,M是边CD上一点,将△ADM沿直线AM对折,得到△ANM.
(1)当AN平分∠MAB时,求DM的长;
(2)连接BN,当DM=1时,求△ABN的面积;
(3)当射线BN交线段CD于点F时,求DF的最大值.

参考答案:
【答案】(1)DM=![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)由折叠可知:△ANM≌△ADM,∠MAN=∠DAM,由AN平分∠MAB,得到∠MAN=∠NAB,进一步有∠DAM=∠MAN=∠NAB.由四边形ABCD是矩形,得到∠DAM=30°,由DM=ADtan∠DAM得到DM的长;
(2)如图1,延长MN交AB延长线于点Q,∵由四边形ABCD是矩形,得到∠DMA=∠MAQ.由折叠可知:△ANM≌△ADM,∠DMA=∠AMQ,得到∠MAQ=∠AMQ,故MQ=AQ.
设NQ=x,则AQ=MQ=1+x.在Rt△ANQ中,由![]() ,得到x=4.
,得到x=4.
故NQ=4,AQ=5,由![]() =
=![]() =
=![]() ANNQ,即可得到结论;
ANNQ,即可得到结论;
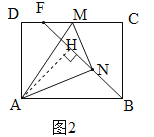
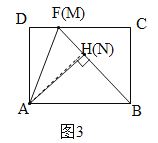
(3)如图2,过点A作AH⊥BF于点H,则△ABH∽△BFC,故![]() .由AH≤AN=3,AB=4,故当点N、H重合(即AH=AN)时,DF最大.此时M、F重合,B、N、M三点共线,△ABH≌△BFC(如图3),而CF=BH=
.由AH≤AN=3,AB=4,故当点N、H重合(即AH=AN)时,DF最大.此时M、F重合,B、N、M三点共线,△ABH≌△BFC(如图3),而CF=BH=![]() =
=![]() ,故课求出DF的最大值.
,故课求出DF的最大值.
试题解析:(1)由折叠可知:△ANM≌△ADM,∴∠MAN=∠DAM,∵AN平分∠MAB,∴∠MAN=∠NAB,∴∠DAM=∠MAN=∠NAB.∵四边形ABCD是矩形,∴∠DAB=90°,∴∠DAM=30°,∴DM=ADtan∠DAM=![]() =
=![]() ;
;
(2)如图1,延长MN交AB延长线于点Q,∵四边形ABCD是矩形,∴AB∥DC,∴∠DMA=∠MAQ.由折叠可知:△ANM≌△ADM,∴∠DMA=∠AMQ,AN=AD=3,MN=MD=1,∴∠MAQ=∠AMQ,∴MQ=AQ.
设NQ=x,则AQ=MQ=1+x.在Rt△ANQ中, ![]() ,∴
,∴![]() ,解得:x=4.
,解得:x=4.
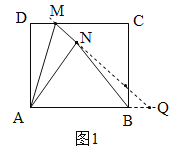
∴NQ=4,AQ=5,∵AB=4,AQ=5,∴![]() =
==
![]() ANNQ=
ANNQ=![]() ;
;
(3)如图2,过点A作AH⊥BF于点H,则△ABH∽△BFC,∴![]() .∵AH≤AN=3,AB=4,∴当点N、H重合(即AH=AN)时,DF最大.(AH最大,BH最小,CF最小,DF最大)
.∵AH≤AN=3,AB=4,∴当点N、H重合(即AH=AN)时,DF最大.(AH最大,BH最小,CF最小,DF最大)
此时M、F重合,B、N、M三点共线,△ABH≌△BFC(如图3),∴CF=BH=![]() =
=![]() =
=![]() ,∴DF的最大值为:
,∴DF的最大值为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2+3x﹣a=0的一个根为﹣1,则另一个根为( )
A.﹣2
B.2
C.4
D.﹣3 -
科目: 来源: 题型:
查看答案和解析>>【题目】2019年“五一”假期期间,我市共接待国内、外游客140.42万人次,实现旅游综合收入8.94亿元,则“旅游综合收入”用科学记数法表示正确的是( )
A. 1.4042×106B. 14.042×105C. 8.94×108D. 0.894×109
-
科目: 来源: 题型:
查看答案和解析>>【题目】向东行进-100m表示的意义是( ).
A. 向东行进100m B. 向南行进100m C. 向北行进100m D. 向西行进100m
-
科目: 来源: 题型:
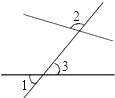
查看答案和解析>>【题目】如图,如果∠1=40°,∠2=100°,那么∠3的同位角等于 度,∠3的内错角等于 度,∠3的同旁内角等于 度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个多边形除了一个内角外,其余各内角之和是2570°,则这个角是( )
A. 90° B. 15° C. 120° D. 130°
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个数是9,另一个数比9的相反数大2,那么这两个数的和为( )
A.2
B.﹣2
C.20
D.﹣20
相关试题

