【题目】已知:![]() 为
为![]() 的直径,
的直径,![]() 为
为![]() 延长线上的任意一点,过点
延长线上的任意一点,过点![]() 作
作![]() 的切线,切点为
的切线,切点为![]() ,
,![]() 的平分线
的平分线![]() 与
与![]() 交于点
交于点![]() .
.
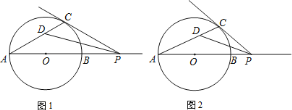
(1)如图![]() ,若
,若![]() 恰好等于
恰好等于![]() ,求
,求![]() 的度数;
的度数;
(2)如图![]() ,若点
,若点![]() 位于
位于![]() 中不同的位置,
中不同的位置,![]() 的结论是否仍然成立?说明你的理由.
的结论是否仍然成立?说明你的理由.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() 的大小不发生变化.理由见解析.
的大小不发生变化.理由见解析.
【解析】
(1)连接OC,则∠OCP=90°,根据∠CPA=30°,求得∠COP,再由OA=OC,得出∠A=∠ACO,由PD平分∠APC,即可得出∠CDP=45°.
(2)由PC是⊙O的切线,得∠OCP=90°.再根据PD是∠CPA的平分线,得∠APC=2∠APD.根据OA=OC,可得出∠A=∠ACO,即∠COP=2∠A,在Rt△OCP中,∠OCP=90°,则∠COP+∠OPC=90°,从而得出∠CDP=∠A+∠APD=45°.所以∠CDP的大小不发生变化.
![]() 连接
连接![]() ,
,
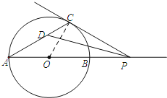
∵![]() 是
是![]() 的切线,
的切线,
∴![]()
∴![]() .
.
∵![]() ,
,
∴![]()
∵![]() ,
,
∴![]()
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)![]() 的大小不发生变化.
的大小不发生变化.
∵![]() 是
是![]() 的切线,
的切线,
∴![]() .
.
∵![]() 是
是![]() 的平分线,
的平分线,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
即![]() 的大小不发生变化.
的大小不发生变化.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店经销一种成本为每千克
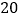 元的水产品,据市场分析,若按每千克
元的水产品,据市场分析,若按每千克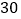 元销售,一个月能售出
元销售,一个月能售出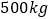 ,销售单价每涨(或跌)
,销售单价每涨(或跌)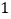 元,月销售量就减少(或增加)
元,月销售量就减少(或增加)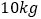 ,解答以下问题:
,解答以下问题:(1)当销售单价定位每千克
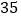 元时,计算月销售量和月销售利润;
元时,计算月销售量和月销售利润;(2)商店想在月销售成本不超过
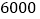 元的情况下,使得月销售利润达到
元的情况下,使得月销售利润达到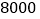 元,销售单价应为多少?
元,销售单价应为多少?(3)商店要使得月销售利润达到最大,销售单价应为多少?此时利润为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的三个顶点分别为A(-1,4),B(-5,3),C(-3,2).
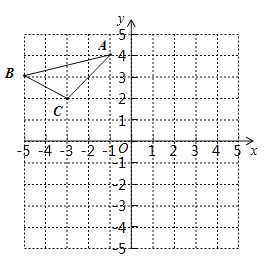
(1)将△ABC向下平移6个单位后得到△A1B1C1,请在图中画出△A1B1C1,并写出C1点坐标;
(2)图中点A2(1,2)与点A关于直线l成轴对称,请在图中画出直线l及△ABC关于直线l对称的△A2B2C2,并写出B2点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,可以自由转动的转盘被它的两条直径分成了四个分别标有数字的扇形区域,其中标有数字“1”的扇形圆心角为120°.转动转盘,待转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转出的数字,此时,称为转动转盘一次(若指针指向两个扇形的交线,则不计转动的次数,重新转动转盘,直到指针指向一个扇形的内部为止)
(1)转动转盘一次,求转出的数字是-2的概率;
(2)转动转盘两次,用树状图或列表法求这两次分别转出的数字之积为正数的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在某次足球训练中,一队员在距离球门12米处挑射,正好射中了2.4米高的球门横梁.若足球运行的路线是抛物线y=ax2+bx+c(如图).现有四个结论:①a﹣b>0;②a<﹣
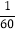 ;③﹣
;③﹣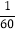 <a<0;④0<b<﹣12a.其中正确的结论是( )
<a<0;④0<b<﹣12a.其中正确的结论是( )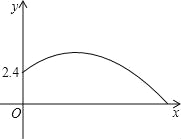
A. ①③ B. ①④ C. ②③ D. ②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数y=kx2+(3k+2)x+1,对于任意负实数k,当x<m时,y随x的增大而增大,则m的最大整数值为( )
A. 2 B. ﹣2 C. ﹣1 D. 0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,BC=8,点P由点B向点A运动,同时,点Q由点C出发沿线段AC的延长线运动,已知点P、Q运动速度相等,点Q与线段BC相交于点D,过点P作PE∥AQ,交BC于点E.
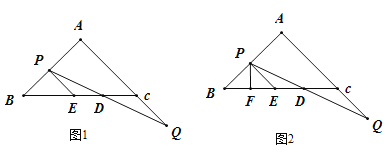
(1)如图1,求证:D为CE中点;
(2)如图2,过点P作PF⊥BC,垂足为点F,在P、Q的运动过程中,请判断DF的长度是否为定值;若是,请求出DF的长度;若否,请说明理由.
相关试题

