【题目】先阅读,再回答问题:要比较代数式A、B的大小,可以作差A﹣B,比较差的取值,当A﹣B>0时,有A>B;当A﹣B=0时,有A=B;当A﹣B<0时,有A<B.”例如,当a<0时,比较a2和a(a+1)的大小.可以观察a2﹣a(a+1)=a2﹣a2﹣a=﹣a.因为当a<0时,﹣a>0,所以当a<0时,a2>a(a+1).
(1)已知M=(x﹣2)(x﹣16),N=(x﹣4)(x﹣8),比较M、N的大小关系.
(2)某种产品的原料提价,因而厂家决定对于产品进行提价,现有三种方案: 方案1:第一次提价p%,第二次提价q%;
方案2:第一次提价q%,第二次提价p%;
方案3:第一、二次提价均为 ![]() %.
%.
如果设原价为a元,请用含a、p、q的式子表示提价后三种方案的价格.
方案1:;方案2:;方案3:
如果p,q是不相等的正数,三种方案哪种提价最多?
参考答案:
【答案】
(1)解:∵M=(x﹣2)(x﹣16)=x2﹣18x+32,N=(x﹣4)(x﹣8)=x2﹣12x+32,
∴M﹣N=(x2﹣18x+32)﹣(x2﹣12x+32)=﹣6x,
∴当x>0时,﹣6x<0,M<N;
当x=0时,﹣6x=0,M=N;
当x<0时,﹣6x>0,M>N.
(2)a(1+p%)(1+q%);a(1+p%)(1+q%);a(1+ ![]() %)2
%)2
【解析】解:方案1:a(1+p%)(1+q%); 方案2:a(1+p%)(1+q%);
方案3:a(1+ ![]() %)2 .
%)2 .
设p%=m,q%=n,则提价后三种方案的价格分别为:
方案1:a(1+m)(1+n)=a(1+m+n+mn);
方案2:a(1+m)(1+n)=a(1+m+n+mn);
方案3:a(1+ ![]() )2=a(1+m+n+
)2=a(1+m+n+ ![]() ).
).
a(1+m+n+ ![]() )﹣a(1+m+n+mn),
)﹣a(1+m+n+mn),
=a(1+m+n+ ![]() ﹣1﹣m﹣n﹣mn),
﹣1﹣m﹣n﹣mn),
=a( ![]() ﹣mn),
﹣mn),
= ![]() (m﹣n)2 ,
(m﹣n)2 ,
∵p≠q,
∴m≠n,
∴ ![]() (m﹣n)2>0,
(m﹣n)2>0,
∴方案3提价最多.
所以答案是:a(1+p%)(1+q%);a(1+p%)(1+q%);a(1+ ![]() %)2 .
%)2 .
【考点精析】解答此题的关键在于理解因式分解的应用的相关知识,掌握因式分解是整式乘法的逆向变形,可以应用与数字计算、求值、整除性问题、判断三角形的形状、解方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察列数:﹣2,8,﹣32,128……按照这列数的排列规律,第n个数应该是( )
A.(﹣2)nB.(﹣2)2n﹣1C.﹣22n﹣1D.(﹣1)n22n﹣1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,M是铁丝AD的中点,将该铁丝首尾相接折成△ABC,且∠B=30°,∠C=100°,如图2.则下列说法正确的是( )

A.点M在AB上
B.点M在BC的中点处
C.点M在BC上,且距点B较近,距点C较远
D.点M在BC上,且距点C较近,距点B较远
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:a2﹣4= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在﹣1,0,﹣2,1这四个数中,最小的数是( )
A.﹣2
B.﹣1
C.0
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角三角形纸片的两直角边长分别为6、8,按如图那样折叠,使点A与点B重合,折痕为DE,则S△BCE:S△BDE等于( )
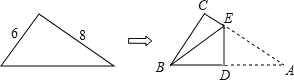
A.2:5 B.14:25 C.16:25 D.4:21
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是某村一遍若干亩土地的示意图,在党的“十六大”精神的指导下,为进一步加大农村经济结构调整的力度,某村决定把这块土地平均分给四位“花农”种植,请你帮他们分一分,提供两种分法.要求:画出图形,并简要说明分法.
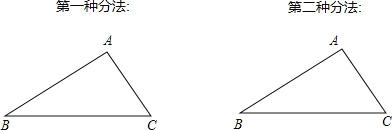
相关试题

