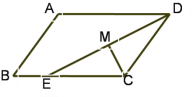
【题目】在平行四边形ABCD中,∠C和∠D的平分线交于M,DM的延长线交AD于E,试猜想:
(1)CM与DE的位置关系?
(2)M在DE的什么位置上?并证明你的猜想.
参考答案:
【答案】(1) CM⊥DE;(2)M为ED的中点,见解析.
【解析】
(1)CM⊥DE,由平行四边形ABCD得AD∥BC,∠ADC+∠BCD=180°,结合角平分线可得∠MDC+∠MCD=90°,即可得结论;
(2)由平行线的性质得∠ADE=∠CEM,结合角平分线可得∠CDE=∠CED,可证出△ECD是等腰三角形,利用等腰三角形三线合一可得CM是中线,则M为ED的中点.
(1) CM⊥DE
∵ AD∥BC
∴∠ADC+∠BCD=180°
∵DE,CM分别平分∠ADC, ∠BCD
∴∠MDC+∠MCD=90°
∴CM⊥DE
(2)M为ED的中点
∵AD∥BC
∴∠ADE=∠CEM
∵∠ADE=∠CDE
∴∠CDE=∠CED
∴CD=CE
∵CM⊥DE,
∴EM=MD,即M为ED的中点.
故答案为:(1) CM⊥DE;(2)M为ED的中点,见解析.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x、y轴的正半轴上,顶点B的坐标为(4,2).点M是边BC上的一个动点(不与B、C重合),反比例函数y=
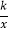 (k>0,x>0)的图象经过点M且与边AB交于点N,连接MN.
(k>0,x>0)的图象经过点M且与边AB交于点N,连接MN.(1)当点M是边BC的中点时.
①求反比例函数的表达式;
②求△OMN的面积;
(2)在点M的运动过程中,试证明:
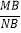 是一个定值.
是一个定值.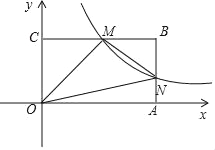
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(1,0)、C(﹣2,3)两点,与y轴交于点N,其顶点为D.
(1)求抛物线及直线AC的函数关系式;
(2)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值及此时点P的坐标;
(3)在对称轴上是否存在一点M,使△ANM的周长最小.若存在,请求出M点的坐标和△ANM周长的最小值;若不存在,请说明理由.

-
科目: 来源: 题型:
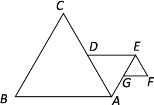
查看答案和解析>>【题目】如图,作等边△ABC,取AC的中点D,以AD为边向△ABC形外作等边△ADE,取AE的中点G,再以EG为边作等边△EFG,如此反复,当作出第6个三角形时,若AB=4,整个图形的外围周长是______.
-
科目: 来源: 题型:
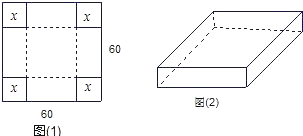
查看答案和解析>>【题目】用一块边长为60㎝的正方形薄钢片制作一个长方体盒子:如果要做成一个没有盖的长方体盒子,可先在薄钢片的四个角上截去四个相同的小正方形,如图(1),然后把四边折合起来,如图(2)
(1)求做成的盒子底面积y(㎝2)与截去小正方形边长x(㎝)之间的函数关系式;
(2)当做成的盒子的底面积为900㎝2时,试求该盒子的容积.
-
科目: 来源: 题型:
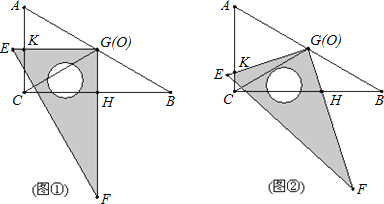
查看答案和解析>>【题目】把两个全等的直角三角板ABC和EFG叠放在一起,使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合,其中∠B=∠F=30°,斜边AB和EF长均为4.
(1)当 EG⊥AC于点K,GF⊥BC于点H时(如图①),求GH:GK的值.
(2) 现将三角板EFG由图①所示的位置绕O点沿逆时针方向旋转,旋转角α满足条件:0°<α<30°(如图②),EG交AC于点K ,GF交BC于点H,GH:GK的值是否改变?证明你发现的结论;
(3)三角板EFG由图①所示的位置绕O点逆时针旋转一周,是否存在某位置使△BFG是等腰三角形,若存在,请直接写出相应的旋转角α(精确到0.1°);若不存在,说明理由.
-
科目: 来源: 题型:
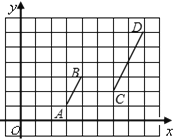
查看答案和解析>>【题目】线段AB、CD在平面直角坐标系中位置如图所示,O为坐标原点.若线段AB上一点P的坐标为(a、b),则直线OP与线段CD的交点坐标为_______.
相关试题

