【题目】如图,点P是四边形ABCD外接圆上任意一点,且不与四边形顶点重合,若AD是⊙O的直径,AB=BC=CD.连接PA,PB,PC,若PA=a,则点A到PB和PC的距离之和AE+AF= . 
参考答案:
【答案】![]() a
a
【解析】解:如图,连接OB、OC.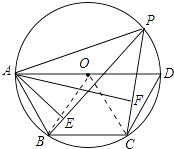
∵AD是直径,AB=BC=CD,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴∠AOB=∠BOC=∠COD=60°,
∴∠APB= ![]() ∠AOB=30°,∠APC=
∠AOB=30°,∠APC= ![]() ∠AOC=60°,
∠AOC=60°,
在Rt△APE中,∵∠AEP=90°,
∴AE=APsin30°= ![]() a,
a,
在Rt△APF中,∵∠AFP=90°,
∴AF=APsin60°= ![]() a,
a,
∴AE+AF= ![]() a.
a.
所以答案是 ![]() a.
a.
【考点精析】关于本题考查的勾股定理的概念和圆周角定理,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果将四根木条首尾相连,在相连处用螺钉连接,就能构成一个平面图形.
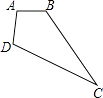
(1)若固定三根木条AB,BC,AD不动,AB=AD=2cm,BC=5cm,如图,量得第四根木条CD=5cm,判断此时∠B与∠D是否相等,并说明理由.
(2)若固定一根木条AB不动,AB=2cm,量得木条CD=5cm,如果木条AD,BC的长度不变,当点D移到BA的延长线上时,点C也在BA的延长线上;当点C移到AB的延长线上时,点A、C、D能构成周长为30cm的三角形,求出木条AD,BC的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知Rt△ABC中,∠B=90°,AC=20,AB=10,P是边AC上一点(不包括端点A、C),过点P作PE⊥BC于点E,过点E作EF∥AC,交AB于点F.设PC=x,
PE=y.
(1)求y与x的函数关系式;
(2)是否存在点P使△PEF是Rt△?若存在,求此时的x的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,函数
 与
与 图象的交于点A,
图象的交于点A, 若点A的坐标为
若点A的坐标为 .
. 点B的坐标为______;
点B的坐标为______; 若点P为第一象限内双曲线上不同于点B的任意一点.
若点P为第一象限内双曲线上不同于点B的任意一点. 设直线PA交x轴于点M,直线PB交x轴于点N,求证
设直线PA交x轴于点M,直线PB交x轴于点N,求证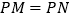 ;
; 当P的坐标为
当P的坐标为 时,连结PO延长交
时,连结PO延长交 于C,求证四边形PACB为矩形.
于C,求证四边形PACB为矩形.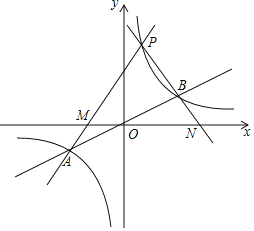
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=AD,CB=CD,对角线AC,BD相交于点O,下列结论中:
①∠ABC=∠ADC;
②AC与BD相互平分;
③AC,BD分别平分四边形ABCD的两组对角;
④四边形ABCD的面积S=
 ACBD.
ACBD.正确的是 (填写所有正确结论的序号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】顺次连接菱形各边的中点所形成的四边形是( )
A.等腰梯形
B.矩形
C.菱形
D.正方形
相关试题

