【题目】把棱长为1cm的若干个小正方体摆放成如图所示的几何体,然后在露出的表面上涂上颜色(不含底面)
(1)该几何体中有 小正方体?
(2)其中两面被涂到的有 个小正方体;没被涂到的有 个小正方体;
(3)求出涂上颜色部分的总面积.

参考答案:
【答案】(1)14;(2)4,1;(3)33cm2
【解析】
(1)该几何体中正方体的个数为最底层的9个,加上第二层的4个,再加上第三层的1个;(2)根据图中小正方体的位置解答即可;(3)涂上颜色部分的总面积可分上面,前面,后面,左面,右面,相加即可.
(1)该几何体中正方体的个数为9+4+1=14个;
(2)根据图中小正方体的位置可知:最底层外边中间的小正方体被涂到2个面,共4个,只有最底层正中间的小正方体没被涂到,
故答案为:4;1;
(3)先算侧面--底层12个小面; 中层8个小面; 上层4个小面;
再算上面--上层1个 中层3个(正方体是可以移动的,不管放在哪里,它压住的面积总是它的底面积,也就是一个,所以中层是4减1个)底层(9-4)=5个,
∴总共12+8+4+1+3+5=33个小面.
∴涂上颜色部分的总面积=1![]() 1
1![]() 33=33cm2.
33=33cm2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线l1:y=﹣x2+2x+3与x轴交于点A,B(点A在点B左边),与y轴交于点C,抛物线l2经过点A,与x轴的另一个交点为E(4,0),与y轴交于点D(0,﹣2).

(1)求抛物线l2的解析式;
(2)点P为线段AB上一动点(不与A、B重合),过点P作y轴的平行线交抛物线l1于点M,交抛物线l2于点N.
①当四边形AMBN的面积最大时,求点P的坐标;
②当CM=DN≠0时,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,点E、F分别是AD、AB的中点,EF交AC于点G,那么AG:GC的值为( )

A.1:2
B.1:3
C.1:4
D.2:3 -
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x,y的二元一次方程组
 的解是一个等腰三角形的一条腰和一条底边的长,且这个等腰三角形的周长为9,求m的值.
的解是一个等腰三角形的一条腰和一条底边的长,且这个等腰三角形的周长为9,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】华联超市用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的
 多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)甲
乙
进价(元/件)
22
30
售价(元/件)
29
40
(1)该商场购进甲、乙两种商品各多少件?
(2)该超市将购进的甲、乙两种商品全部卖完后一共可获得多少利润?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,真命题是( )
A. 如果三角形三个角的度数比是3:4:5,那么这个三角形是直角三角形
B. 如果直角三角形两直角边的长分别为a和b,那么斜边的长为a2+b2
C. 若三角形三边长的比为1:2:3,则这个三角形是直角三角形
D. 如果直角三角形两直角边分别为a和b,斜边为c,那么斜边上的高h的长为
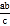
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段AB上有一任意点C,点M是线段AC的中点,点N是线段BC的中点,当AB=6cm时,
(1)求线段MN的长.
(2)当C在AB延长线上时,其他条件不变,求线段MN的长.

相关试题

