【题目】在平面直角坐标系中,点A(-1,-2),B(5,4).已知抛物线y=x2-2x+c与线段AB有公共点,则c的取值范围是________.
参考答案:
【答案】-11≤c≤![]()
【解析】抛物线y=x2-2x+c与y轴的交点坐标为(0,c).
如解图,抛物线的对称轴为直线x=1,
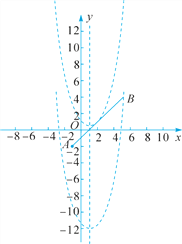
易求得直线AB的函数表达式为y=x-1.
当直线AB与抛物线y=x2-2x+c只有一个公共点,即方程x2-2x+c=x-1的Δ=0时,抛物线y=x2-2x+c与y轴的交点最高,即c的值最大,此时9-4(c+1)=0,解得c=![]() .
.
当抛物线y=x2-2x+c过点B时,抛物线y=x2-2x+c与y轴的交点最低,即c的值最小,
把点B(5,4)的坐标代入y=x2-2x+c,得25-10+c=4,解得c=-11.
∴C的取值范围是-11≤c≤![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,ABCD中,对角线AC、BD交于点O,直线EF经过点O,分别交DA,BC的延长线于点E,F,连接BE,DF.
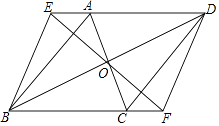
求证:
(1)AE=CF;
(2)四边形BEDF是平行四边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】在下列多项式中,与-x-y相乘的结果为x2-y2的多项式是
A. -x+yB. x+yC. x-yD. -x-y
-
科目: 来源: 题型:
查看答案和解析>>【题目】PM2.5是大气压中直径小于或等于0.0000025m的颗粒物,将0.0000025用科学记数法表示为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各图能表示y是x的函数是( )
A.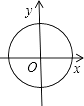
B.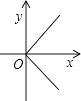
C.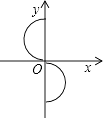
D.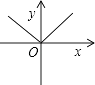
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一组数据:3,5,5,6,7,这组数据的众数为( )
A.3
B.5
C.6
D.7 -
科目: 来源: 题型:
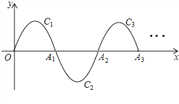
查看答案和解析>>【题目】如图,一段抛物线:y=﹣x(x﹣3)(0≤x≤3),记为C1,它与x轴交于点O,A1;
将C1绕点A1旋转180°得C2,交x轴于点A2;
将C2绕点A2旋转180°得C3,交x轴于点A3;
…
如此进行下去,直至得C13.若P(37,m)在第13段抛物线C13上,则m=_____.
相关试题

