搜索
【题目】下列语句中正确的有（ ）
①经过一点，有且只有一条直线与已知直线平行；②有公共顶点且和为
的两个角是邻补角；③两条直线被第三条直线所截，同旁内角互补；④不相交的两条直线叫做平行线；⑤直线外的一点到已知直线的垂线段叫做点到直线的距离；
A.0个；B.1个；C.2个；D.3个；
参考答案：
【答案】A
【解析】
根据平行公理、邻补角的概念、平行线的性质和概念、点到直线的距离的概念逐一判断即可.
解：经过直线外一点，有且只有一条直线与已知直线平行，故①错误；
两直线互相垂直，由两对90°的对顶角，满足有公共顶点且和为180°，但它们不是邻补角，故②错误；
两条平行直线被第三条直线所截，同旁内角互补，故③错误；
同一平面内，不相交的两条直线叫做平行线，故④错误；
直线外的一点到已知直线的垂线段的长度叫做点到直线的距离，故⑤错误；
综上，正确的个数为0，故答案为A.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校开展“我最喜爱的一项体育活动”调查，要求每名学生必选且只能选一项，现随机抽查了m名学生，并将其结果绘制成如下不完整的条形图和扇形图．
请结合以上信息解答下列问题：
（1）m= ；
（2）请补全上面的条形统计图；
（3）在图2中，“乒乓球”所对应扇形的圆心角的度数为 ；
（4）已知该校共有1200名学生，请你估计该校约有 名学生最喜爱足球活动．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为加快“秀美荆河水系生态治理工程”进度，污水处理厂决定购买10台污水处理设备．现有A，B两种型号的设备，每台的价格分别为a万元，b万元，每月处理污水量分别为240吨，200吨．已知购买一台A型设备比购买一台B型设备多2万元，购买2台A型设备比购买3台B型设备少6万元．
（1）求a，b的值；
（2）厂里预算购买污水处理设备的资金不超过105万元，你认为有哪几种购买方案；
（3）在（2）的条件下，若每月要求处理污水量不低于2040吨，为了节约资金，请你为污水处理厂设计一种最省钱的购买方案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为保护环境，我市公交公司计划购买A型和B型两种环保节能公交车共10辆．若购买A型公交车1辆，B型公交车2辆，共需400万元；若购买A型公交车2辆，B型公交车1辆，共需350万元．
（1）求购买A型和B型公交车每辆各需多少万元？
（2）预计在某线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次．若该公司购买A型和B型公交车的总费用不超过1200万元，且确保这10辆公交车在该线路的年均载客总和不少于680万人次，则该公司有哪几种购车方案？
（3）在（2）的条件下，哪种购车方案总费用最少？最少总费用是多少万元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】按下列要求画图（不需书写结论）并填空;如右图，
（1）过点Q作QD⊥AB，垂足为D，
（2）过点Q作QE∥AB，交AC于点E，
（3）过点Q作QF⊥直线 AC，垂足为F，
（4）联结A、Q两点，
（5）点Q到直线AC的距离是线段 的长度，
（6）直线QE与直线AB之间的距离是线段 的长度.
-
科目： 来源： 题型：
查看答案和解析>>【题目】几何探究题
(1)发现：在平面内，若BC＝a，AC＝b，其中a＞b．
当点A在线段BC上时(如图1)，线段AB的长取得最小值，最小值为 ；
当点A在线段BC延长线上时(如图2)，线段AB的长取得最大值，最大值为 ．
(2)应用：点A为线段BC外一动点，如图3，分别以AB、AC为边，作等边△ABD和等边△ACE，连接CD、BE．
①证明：CD＝BE；
②若BC＝3，AC＝1，则线段CD长度的最大值为 ．
(3)拓展：如图4，在平面直角坐标系中，点A的坐标为(2，0)，点B的坐标为(5，0)，点P为线AB外一动点，且PA＝2，PM＝PB，∠BPM＝90°．请直接写出线段AM长的最大值及此时点P的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，把
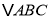的三边BA、CB和AC分别向外延长一倍，将得到的点
，
， 
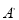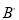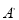
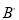
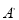
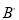
顺次连接成△，若△ABC的面积是3，则△的面积是（ ）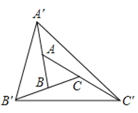
A.15B.18C.21D.24
相关试题
