【题目】我县各中小学校积极组织学生开展课外阅读活动,为了解某校学生每周课外阅读的时间量t(单位:小时),采用随机抽样的方法抽取部分学生进行了问卷调查,调查结果按0≤t〈2,2≤t〈3,3≤t〈4,t≥4分为四个等级,并分别用A、B、C、D表示.根据调查结果统计数据绘制成如图所示的两幅不完整的统计图,由图中给出的信息解答下列问题:
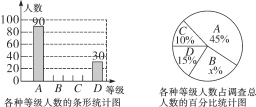
(1)求这次抽查的学生总数是多少人,并求出x的值;
(2)将不完整的条形统计图补充完整;
(3)若该校共有学生3600人,试估计每周课外阅读时间量满足2≤t〈4的人数.
参考答案:
【答案】(1) x=30;(2)补图如图所示见解析; (3)估计每周课外阅读时间量满足2≤t〈4的人数为1440人.
【解析】(1)根据所有等级的百分比的和为1,则可计算出x的值,由条形图可知A等级有90人,由扇形图可知对应的百分比为45%,那么抽查的学生总数=A等级的人数÷对应的百分比,计算即可求解;
(2)根据所有等级的百分比的和为1,则可计算出x的值,再求出B级与C级的人数,即可作图;
(3)利用每周课外阅读时间量满足2≤t<4的人数=该校总人数×B级的与C级百分比的和计算即可.
(1)这次抽查的学生总数是90÷45%=200(人).
由扇形统计图所得x%=100%-45%-15%-10%=30%,即x=30.
(2)补图如图所示.
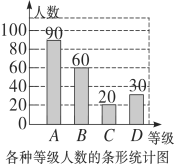
(3)3600×(30%+10%)=1440(人),
即估计每周课外阅读时间量满足2≤t〈4的人数为1440人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某物流公司引进A,B两种机器人用来搬运某种货物,这两种机器人充满电后可以连续搬运5小时,A种机器人于某日0时开始搬运,过了1小时,B种机器人也开始搬运,如图,线段OG表示A种机器人的搬运量yA(千克)与时间x(时)的函数图象,根据图象提供的信息,解答下列问题:

(1)求yB关于x的函数解析式;
(2)如果A,B两种机器人连续搬运5小时,那么B种机器人比A种机器人多搬运了多少千克?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,直线AB∥CD
(1)如图1,点E在直线BD的左侧,猜想∠ABE、∠CDE、∠BED的数量关系,并证明你的结论;
(2)如图2,点E在直线BD的左侧,BF、DF分别平分∠ABE、∠CDE,猜想∠BFD和∠BED的数量关系,并证明你的结论;
(3)如图3,点E在直线BD的右侧,BF、DF分别平分∠ABE、∠CDE;那么第(2)题中∠BFD和∠BED的数量关系的猜想是否仍成立?如果成立,请证明;如果不成立,请写出你的猜想,并证明.



-
科目: 来源: 题型:
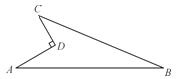
查看答案和解析>>【题目】有一块空白地,如图,∠ADC=90°,CD=6 m,AD=8 m,AB=26 m,BC=24 m.试求这块空白地的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,对称轴为直线x=2的抛物线y=x2+bx+c与x轴交于点A和点B,与y轴交于点C,且点A的坐标为(﹣1,0)
注:二次函数y=ax2+bx+c(a≠0)的顶点坐标为(﹣ ,
,  )
)
(1)求抛物线的解析式;
(2)直接写出B、C两点的坐标;
(3)求过O,B,C三点的圆的面积.(结果用含π的代数式表示) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=BC,P是△ABC内一点,且PA=3,PB=1,PC= CD=2,CD⊥CP,求∠BPC的度数

-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)某商场用2500元购进了A、B两种新型节能台灯共50盏,这两种台灯的进价,标价如下表所示:

(1)这两种台灯各购进多少盏?
(2)若A型台灯按标价的九折出售,B型台灯按标价的八折出售,那么这批台灯全部售完后,商场共获利多少元?
相关试题

