【题目】如图,已知⊙O是以BC为直径的△ABC的外接圆,OP∥AC,且与BC的垂线交于点P,OP交AB于点D,BC、PA的延长线交于点E. 
(1)求证:PA是⊙O的切线;
(2)若sinE= ![]() ,PA=6,求AC的长.
,PA=6,求AC的长.
参考答案:
【答案】
(1)证明:连接OA,如图,

∵AC∥OP,
∴∠ACO=∠POB,∠CAO=∠POA,
又∵OA=OC,
∴∠ACO=∠CAO,
∴∠POA=∠POB,
在△PAO和△PBO中,
 ,
,
∴△PAO≌△PBO(SAS),
∴∠PAO=∠PBO,
又∵PB⊥BC,
∴∠PBO=90°,
∴∠PAO=90°,
∴OA⊥PE,
∴PA是⊙O的切线
(2)解:∵△PAO≌△PBO,
∴PB=PA=6,
在Rt△PBE中,∵sinE= ![]() =
= ![]()
∴ ![]() =
= ![]() ,解得PE=10,
,解得PE=10,
∴AE=PE﹣PA=4,
在Rt△AOE中,sinE= ![]() =
= ![]() ,
,
设OA=3t,则OE=5t,
∴AE= ![]() =4t,
=4t,
∴4t=4,解得t=1,
∴OA=3,
在Rt△PBO中,∵OB=3,PB=6,
∴OP= ![]() =3
=3 ![]() ,
,
∵AC∥OP,
∴△EAC∽△EPO,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴AC= ![]() .
.
【解析】(1)先利用平行线的性质得到∠ACO=∠POB,∠CAO=∠POA,加上∠ACO=∠CAO,则∠POA=∠POB,于是可根据“SAS”判断△PAO≌△PBO,则∠PAO=∠PBO=90°,然后根据切线的判定定理即可得到PA是⊙O的切线;(2)先由△PAO≌△PBO得PB=PA=6,在Rt△PBE中,利用正弦的定义可计算PE=10,则AE=PE﹣PA=4,再在Rt△AOE中,由sinE= ![]() =
= ![]() ,可设OA=3t,则OE=5t,由勾股定理得到AE=4t,则4t=4,解得t=1,所以OA=3;接着在Rt△PBO中利用勾股定理计算出OP=3
,可设OA=3t,则OE=5t,由勾股定理得到AE=4t,则4t=4,解得t=1,所以OA=3;接着在Rt△PBO中利用勾股定理计算出OP=3 ![]() ,然后证明△EAC∽△EPO,再利用相似比可计算出AC.
,然后证明△EAC∽△EPO,再利用相似比可计算出AC.
【考点精析】根据题目的已知条件,利用切线的判定定理的相关知识可以得到问题的答案,需要掌握切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知m为常数,整式(m+2)x2y+mxy2与3x2y的和为单项式.则m=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人到某商店购买A型和B型两种特惠商品,已知甲、乙两人购买A型和B型两种商品的件数和所花钱的总额如下表所示:
A型商品数量(件)
B型商品数量(件)
总额(元)
甲
2
3
43
乙
3
4
60
(1)试求A型和B型两种商品的单价各是多少?
(2)假设两人购买商品的件数相同,且两人共花去了172元,则甲、乙两人购买的所有商品中,A型商品共有几件?B型商品呢?
-
科目: 来源: 题型:
查看答案和解析>>【题目】你会求(a﹣1)(a2014+a2013+a2012+…+a2+a+1)的值吗?这个问题看上去很复杂,我们可以先考虑简单的情况,通过计算,探索规律:
 ;
; ;
; .
.(1)由上面的规律我们可以大胆猜想,得到(a﹣1)(a2014+a2013+a2012+…+a2+a+1)=________
利用上面的结论,求:
(2)22014+22013+22012+…+22+2+1的值是 。
(3)求52014+52013+52012+…+52+5+1的值。
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如图1可以得到(a+b)2=a2+2ab+b2,请解答下列问题:

(1)写出图2中所表示的数学等式 。
(2)根据整式乘法的运算法则,通过计算验证上述等式。
(3)利用(1)中得到的结论,解决下面的问题:
若a+b+c=10,ab+ac+bc=35,则a2+b2+c2= .
(4)小明同学用图3中x张边长为a的正方形,y张边长为b的正方形z张边长分别为a、b的长方形纸片拼出一个面积为(5a+7b)(9a+4b)长方形,则x+y+z= 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+2与直线l交于点A、B两点,且A点为抛物线与y轴的交点,B(﹣2,﹣4),抛物线的对称轴是直线x=2,过点A作AC⊥AB,交抛物线于点C、x轴于点D.

(1)求此抛物线的解析式;
(2)求点D的坐标;
(3)抛物线上是否存在点K,使得以AC为边的平行四边形ACKL的面积等于△ABC的面积?若存在,请直接写出点K的横坐标;若不存在,请说明理由.[提示:抛物线y=ax2+bx+c(a≠0)的对称轴为x=﹣ ,顶点坐标为(﹣
,顶点坐标为(﹣  ,
, 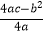 )].
)]. -
科目: 来源: 题型:
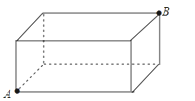
查看答案和解析>>【题目】已知长方体的长、宽、高分别为30cm、20cm、10cm,一只蚂蚁从A处出发到B处觅食,求它所走的最短路径.(结果保留根号)
相关试题

