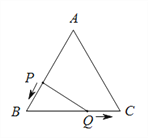
【题目】如图,已知△ABC是边长为3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1 cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间为t(s),则(1)BP![]() cm,BQ
cm,BQ![]() cm.(用含t的代数式表示)
cm.(用含t的代数式表示)
(2)当t为何值时,△PBQ是直角三角形?
参考答案:
【答案】(1)3-t,t;(2)当t=1s或t=2s时,△PBQ是直角三角形.
【解析】分析:(1)根据路程=速度×时间即可求得;(2)根据等边三角形的性质可以知道这个直角三角形∠B=60°,所以就可以表示出BQ与PB的关系,要分情况进行讨论:①∠BPQ=90°;②∠PQB=90°.然后在直角三角形BQP中根据BP,BQ的表达式和∠B的度数进行求解即可.
本题解析:
(1)![]() cm,
cm,![]() cm
cm
在 △PBQ中,![]()
若△PBQ是直角三角形,则点P或点Q
为直角顶点
①若点P为直角顶点,因为![]() ,所以
,所以![]()
所以![]() 即t=2(3-t), 解得t=2
即t=2(3-t), 解得t=2
②若点Q是直角顶点,∵![]() ,∴
,∴![]()
∴![]() 即3-t=2t, 解得t=1
即3-t=2t, 解得t=1
答:当t=1s或t=2s时,△PBQ是直角三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个盒子里有完全相同的三个小球,球上分别标上数字﹣1、1、2.随机摸出一个小球(不放回)其数字记为p,再随机摸出另一个小球其数字记为q,则满足关于x的方程x2+px+q=0有实数根的概率是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中错误的是( )
A.某种彩票的中奖率为1%,买100张彩票一定有1张中奖
B.从装有10个红球的袋子中,摸出1个白球是不可能事件
C.为了解一批日光灯的使用寿命,可采用抽样调查的方式
D.掷一枚普通的正六面体骰子,出现向上一面点数是2的概率是

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知下列单项式:
①4m2,②9b2a,③6a2b,④4n2,⑤-4n2,⑥-12ab,⑦-8mn,⑧a3.
请在以上单项式中选取三个组成一个能够先用提公因式法,再用公式法因式分解的多项式并将这个多项式分解因式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简求值:当5x2+x+2=0时,求2(3x+2y)2 -(x+2y)(2y-x) –(12x2y2-2x2y)÷xy的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),在四边形ABCD中,已知∠ABC
 ∠ADC
∠ADC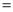 180°,AB
180°,AB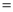 AD,AB
AD,AB AD,点E在CD的延长线上,∠1
AD,点E在CD的延长线上,∠1 ∠2.
∠2.(1)求证:∠3
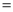 ∠E;
∠E;(2)求证:CA平分∠BCD;
(3)如图(2),设AF是△ABC的边BC上的高,求证:CE
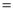 2AF.
2AF.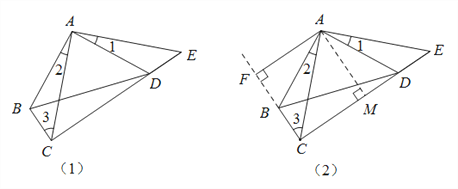
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的布袋里装有4个大小,质地都相同的乒乓球,球面上分别标有数字1,-2,3,-4,小明先从布袋中随机摸出一个球(不放回去),再从剩下的3个球中随机摸出第二个乒乓球.
(1)共有 种可能的结果.
(2)请用画树状图或列表的方法求两次摸出的乒乓球的数字之积为偶数的概率.
相关试题

