【题目】(1)如图1,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 分别是
分别是![]() 上的点,且
上的点,且![]() ,探究图中
,探究图中![]() 之间的数量关系。小明同学探究此问题的方法是:延长
之间的数量关系。小明同学探究此问题的方法是:延长![]() 到点
到点![]() ,使
,使![]() 。连接
。连接![]() ,先证明
,先证明![]() ,再证明
,再证明![]() ,可得出结论。他的结论应是______________________________________(不写过程)。
,可得出结论。他的结论应是______________________________________(不写过程)。
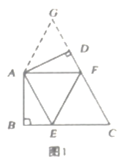
(2)如图2,若在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 分别是
分别是![]() 上的点,且
上的点,且![]() ,上述结论是否仍然成立,并说明理由。
,上述结论是否仍然成立,并说明理由。
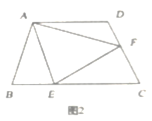
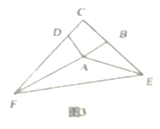
(3)如图3,已知在四边形![]() 中,
中,![]() ,
,![]() ,若点
,若点![]() 在
在![]() 的延长线上,点
的延长线上,点![]() 在
在![]() 的延长线上,仍然满足
的延长线上,仍然满足![]() ,请写出
,请写出![]() 与
与![]() 的数量关系,并给出证明过程。
的数量关系,并给出证明过程。
参考答案:
【答案】(1)![]() ;(2)仍成立,见解析;(3)
;(2)仍成立,见解析;(3)![]() ,见解析
,见解析
【解析】
(1)延长FD到点G,使DG=BE,连接AG,利用SAS可判定△ABE≌△ADG,进而得出∠BAE=∠DAG,AE=AG,再利用SSS判定△AEF≌△AGF,可得出∠EAF=∠GAF=∠DAG+∠DAF=∠BAE+∠DAF,据此得出结论;
(2)延长FD到点G,使DG=BE,连接AG,利用SAS先判定△ABE≌△ADG,进而得出∠BAE=∠DAG,AE=AG,再利用SSS判定△AEF≌△AGF,可得出∠EAF=∠GAF=∠DAG+∠DAF=∠BAE+∠DAF;
(3)在DC延长线上取一点G,使得DG=BE,连接AG,利用SAS先判定△ADG≌△ABE,再利用SSS判定△AEF≌△AGF,得出∠FAE=∠FAG,最后根据∠FAE+∠FAG+∠GAE=360°,推导得到2∠FAE+∠DAB=360°,即可得出结论.
(1)∠BAE+∠FAD=∠EAF.理由:
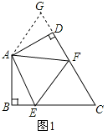
如图1,延长FD到点G,使DG=BE,连接AG,
在![]() ABE和
ABE和![]() ADG中,
ADG中,
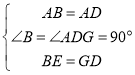
∴△ABE≌△ADG(SAS),
∴EF=FG,AE=AG,![]() BAE=
BAE=![]() DAG
DAG
![]() EF=BE+FD
EF=BE+FD
∴EF=GD+FD=GF
在△EAF和△GAF中,

∴△AEF≌△AGF(SSS),
∴∠EAF=∠GAF=∠DAG+∠DAF=∠BAE+∠DAF.
故答案为:∠BAE+∠FAD=∠EAF;
(2)仍成立,
理由如下:如图,延长![]() 到点
到点![]() ,使
,使![]() ,连接
,连接![]() 、
、

![]()
![]() B+
B+![]() ADF=180,又
ADF=180,又![]() ADG+
ADG+![]() ADF=180,
ADF=180,
∴![]() B=
B=![]() ADG
ADG
在△ABE和△ADG中,
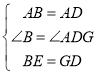
∴△ABE![]() △ADG(SAS),
△ADG(SAS),
∴AE=AG,![]() BAE=
BAE=![]() DAG,
DAG,
![]() EF=BE+FD
EF=BE+FD
∴EF=GD+FD=GF
在△EAF和△GAF中,

∴△EAF![]() △GAF(SSS)
△GAF(SSS)
∴![]() EAF=
EAF=![]() GAF=
GAF=![]() BAE+
BAE+![]() FAD
FAD
∴![]()
(3)![]()
证明:如图,在![]() 的延长线上取一点
的延长线上取一点![]() ,使得
,使得![]() ,连接
,连接![]()
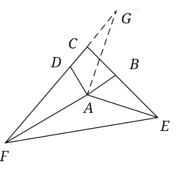
![]()
![]() ABC+
ABC+![]() ADC=180,又
ADC=180,又![]() ABC+
ABC+![]() ABE=180,
ABE=180,
∴![]() ABE=
ABE=![]() ADG
ADG
在△ABE和△ADG中,
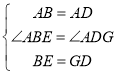
∴△ABE![]() △ADG(SAS),
△ADG(SAS),
∴AE=AG,![]() BAE=
BAE=![]() DAG,
DAG,
![]() EF=BE+FD
EF=BE+FD
∴EF=GD+FD=GF
在△EAF和△GAF中,

∴△EAF![]() △GAF(SSS)
△GAF(SSS)
∴ ![]() 又
又![]()
∴![]()
∴![]() ,
,
∴![]()
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△ABC中,AM为边BC上的中线,动点D在直线AM上,以CD为一边在CD的下方作等边△CDE,设直线BE与直线AM的交点为O.
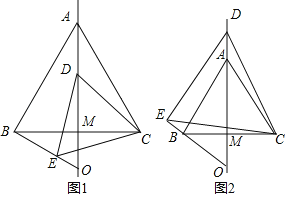
(1)如图1,点D在线段AM上时,填空:
①线段AD与BE的数量关系是 ②∠AOB的度数是 .
(2)如图2,当动点D在线段MA的延长线上时,试判断(1)中的结论是否成立?若成立,请给予证明:若不成立,请写出新的结论,并说明理由.
-
科目: 来源: 题型:
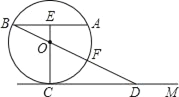
查看答案和解析>>【题目】如图,已知:AB为⊙O的弦(非直径),E为AB的中点,EO的延长线与⊙O相交于C,CM∥AB,BO的延长线与⊙O相交于F,与CM相交于D.
①求证:EC⊥CD;
②当EO:OC=1:3,CD=4时,求⊙O的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C在BA的延长线上,CA=AO,点D在⊙O上,∠ABD=30°.
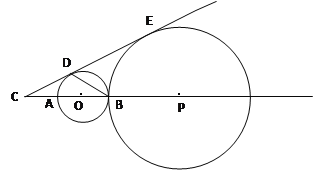
⑴求证:CD是⊙O的切线;
⑵若点P在直线AB上,⊙P与⊙O外切于点B,与直线CD相切于点E,设⊙O与⊙P的半径分别为r与R,求
 的值.
的值. -
科目: 来源: 题型:
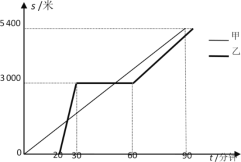
查看答案和解析>>【题目】某景区在同一线路上顺次有三个景点A,B,C,甲、乙两名游客从景点A出发,甲步行到景点C;乙花20分钟时间排队后乘观光车先到景点B,在B处停留一段时间后,再步行到景点C.甲、乙两人离景点A的路程s(米)关于时间t(分钟)的函数图像如图所示.
(1)甲的速度是 米/分钟;
(2)当20≤t ≤30时,求乙离景点A的路程s与t的函数表达式;
(3)乙出发后多长时间与甲在途中相遇?
(4)若当甲到达景点C时,乙与景点C的路程为360米,则乙从景点B步行到景点C的速度是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两位同学参加数学综合素质测试,各项成绩如下(单位:分)
数与代数
空间与图形
统计与概率
综合与实践
学生甲
90
94
86
90
学生乙
94
82
93
91
(1)分别计算甲、乙成绩的平均数和方差;
(2)如果数与代数、空间与图形、统计与概率、综合与实践的成绩按3:3:2:2计算,那么甲、乙的数学综合素质成绩分别为多少分?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P从
 出发,沿所示方向运动,每当碰到长方形OABC的边时会进行反弹,反弹时反射角等于入射角,当点P第2018次碰到长方形的边时,点P的坐标为______.
出发,沿所示方向运动,每当碰到长方形OABC的边时会进行反弹,反弹时反射角等于入射角,当点P第2018次碰到长方形的边时,点P的坐标为______.
【答案】

【解析】
根据反射角与入射角的定义作出图形;由图可知,每6次反弹为一个循环组依次循环,用2018除以6,根据商和余数的情况确定所对应的点的坐标即可.
解:如图所示:经过6次反弹后动点回到出发点
 ,
,
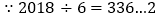 ,
, 当点P第2018次碰到矩形的边时为第337个循环组的第2次反弹,
当点P第2018次碰到矩形的边时为第337个循环组的第2次反弹, 点P的坐标为
点P的坐标为 .
.故答案为:
 .
.【点睛】
此题主要考查了点的坐标的规律,作出图形,观察出每6次反弹为一个循环组依次循环是解题的关键.
【题型】填空题
【结束】
15【题目】为了保护环境,某公交公司决定购买A、B两种型号的全新混合动力公交车共10辆,其中A种型号每辆价格为a万元,每年节省油量为
 万升;B种型号每辆价格为b万元,每年节省油量为
万升;B种型号每辆价格为b万元,每年节省油量为 万升:经调查,购买一辆A型车比购买一辆B型车多20万元,购买2辆A型车比购买3辆B型车少60万元.
万升:经调查,购买一辆A型车比购买一辆B型车多20万元,购买2辆A型车比购买3辆B型车少60万元. 请求出a和b;
请求出a和b; 若购买这批混合动力公交车每年能节省
若购买这批混合动力公交车每年能节省 万升汽油,求购买这批混合动力公交车需要多少万元?
万升汽油,求购买这批混合动力公交车需要多少万元?
相关试题

