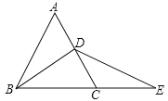
【题目】已知:如图,△ABC是等边三角形,BD⊥AC,E是BC延长线上的一点,且∠CED=30°.
(1)求证:DB=DE.
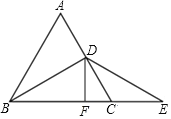
(2)在图中过D作DF⊥BE交BE于F,若CF=3,求△ABC的周长.
参考答案:
【答案】(1)证明见解析;(2)48.
【解析】
试题(1)根据等边三角形的性质得到∠ABC=∠ACB=60°,∠DBC=30°,再根据角之间的关系求得∠DBC=∠CED,根据等角对等边即可得到DB=DE;(2)根据直角三角形中,30°的锐角所对的直角边等于斜边的一半DC=8,AC=16,即可求得△ABC的周长.
试题解析:
(1)证明:∵△ABC是等边三角形,BD是中线,
∴∠ABC=∠ACB=60°.
∠DBC=30°(等腰三角形三线合一).
又∵CE=CD,
∴∠CDE=∠CED.
又∵∠BCD=∠CDE+∠CED,
∴∠CDE=∠CED=![]() ∠BCD=30°.
∠BCD=30°.
∴∠DBC=∠DEC.
∴DB=DE(等角对等边);
(2)解: ∵∠CDE=∠CED=![]() ∠BCD=30°,
∠BCD=30°,
∴∠CDF=30°,
∵CF=4,
∴DC=8,
∵AD=CD,
∴AC=16,
∴△ABC的周长=3AC=48.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC是等边三角形,点D、E分别在AC、BC上,且CD=BE,则∠AFB=_____°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长度为1个单位长度的小正方形组成的正方形中,点A、B、C在小正方形的顶点上.
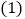 在图中画出与
在图中画出与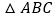 关于直线l成轴对称的
关于直线l成轴对称的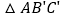 ;
;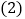 三角形ABC的面积为______;
三角形ABC的面积为______;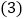 以AC为边作与
以AC为边作与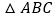 全等的三角形,则可作出______个三角形与
全等的三角形,则可作出______个三角形与 全等;
全等;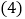 在直线l上找一点P,使
在直线l上找一点P,使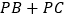 的长最短.
的长最短.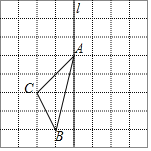
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AC的垂直平分线分别交BC、AC于点D、E.
(1)若AC=12,BC=15,求△ABD的周长;
(2)若∠B=20°,求∠BAD的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在Rt△ABC中,∠C=90°,BC=6cm,AC=8 cm,AB=10 cm. 现有一动点P,从A点出发,沿着三角形的边AC-CB-BA运动,回到A点停止,速度为1 cm/s,设运动时间为t s.
(1)当t=_______时,△ABC的周长被线段AP平分为相等的两部分.
(2)当t=_______时,△APC的面积等于△ABC面积的一半.
(3)还有一个△DEF,∠E=90°,如图②所示,DE=4cm,DF=5cm,∠D=∠A. 在△ABC的边上,若另外有一个动点Q,与P 同时从A点出发,沿着边AB-BC-CA运动,回到点A停止. 在两点运动过程中某一时刻,恰好△APQ与△DEF全等,则点Q的运动速度 cm/s.


-
科目: 来源: 题型:
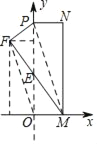
查看答案和解析>>【题目】如图,在平面直角坐标系中,长方形MNPO的边OM在x轴上,边OP在y轴上,点N的坐标为(3,9),将矩形沿对角线PM翻折,N点落在F点的位置,且FM交y轴于点E,那么点F的坐标为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】西安市在创建文明城区的活动中,有两个长度相等的彩色砖道铺设任务,分别交给甲、乙两个施工队同时进行施工,如图是反映所铺设的彩色砖道的长度y(米)与施工时间x(小时)之间关系的部分图象,请解答下列问题:
(1)求乙队在0≤x≤6的时段内y与x的函数关系式.
(2)如果甲队施工速度不变,乙队在施工6小时后,施工速度增加到12米/小时,结果两队同时完成了任务,求甲队从开始施工到完成所铺设的彩色砖道的长度为多少米?

相关试题

