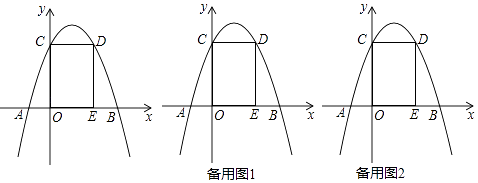
【题目】已知AB为⊙O的直径,BM为⊙O的切线,点C为射线BM上一点,连接AC交⊙O于点D,点E为BC上一点.连接AE交半圆于F.
(1)如图1,若AE平分∠BAC,求证:∠DBF=∠CBF;
(2)如图2,过点D作⊙O的切线交BM于N,若DN⊥BM,求证:△ABC为等腰直角三角形;
(3)在(2)的条件下,如图3,延长BF交AC于G,点H为AB上一点,且BH=2BE,过点H作AE的垂线交AC于P,连接OG交DN于K,若AP=CG,EF=1,求GK的长.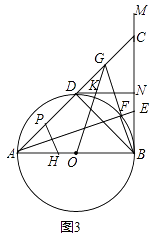
参考答案:
【答案】
(1)解:证明:如图1中,
∵AB是直径,BM是切线,
∴∠AFB=∠ABC=90°,
∵∠FAB+∠ABF=90°,∠ABF+∠CBF=90°,
∴∠CBF=∠FAB,
∵AE平分∠BAC,
∴∠EAC=∠FAB,
∵∠DBF=∠EAC,
∴∠DBF=∠CBF.
(2)解:证明:如图2中,连接DM.
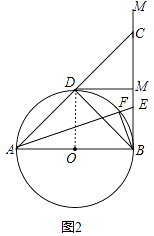
∵DM是⊙O的切线,DM⊥BC,
∴∠ODM=∠DMB=∠OBM=90°,
∴四边形ODMB是矩形,
∵OD=OB,
∴四边形ODMB是正方形,
∴∠DBO=45°,
∵AB是直径,
∴∠ADB=90°,
∴∠DAB=45°,∵∠ABC=90°,
∴∠BAC=∠ACB=45°,
∴△ABC是等腰直角三角形.
(3)解:如图3中,连接PB,作CM⊥BC交HP的延长线于M,延长BG交CM于N,作GR⊥AB于R,交DN于T.
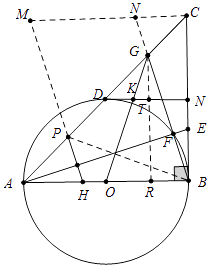
∵AP=CG,∠BAP=∠BCG=45°,BA=BC,
∴△BAP≌△BCG,
∴BP=BG,
∴∠BPG=∠BGP,
∵HM⊥AE,BN⊥AE,
∴HM∥BN,∵MN∥BH,
∴四边形MNBH是平行四边形,
∴MN=BH,
∵∠APH=∠CPM=∠BGP=∠BPG,
PC=PC,∠PCB=∠PCM,
∴△PCM≌△PCB,
∴CM=BC=AB,
∵BC=AB,∠ABE=∠BCN,易证∠BAE=∠CBN,
∴△ABE≌△BCN,
∴BE=CN,设BE=CN=a,则BH=MN=2a,
∴CM=BC=AB=3a,
∴AH=BE=a,
∵△BFE∽△ABE,
∴ ![]() =
= ![]() =
= ![]() ,
,
∵EF=1,
∴BF=3,BE= ![]() =
= ![]() ,
,
∴AH=CN=BE= ![]() ,AB=BC=CM=3
,AB=BC=CM=3 ![]() ,
,
∵AH∥CM,
∴ ![]() =
= ![]() =
= ![]() ,
,
∵AP=CG,
∴AP=DP=DG=CG,
∵GR∥BC,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴AR=GR= ![]() ,OR=RB=
,OR=RB= ![]() ,
,
在Rt△GOR中,GO= ![]() =
= ![]() ,
,
∵DK∥OA,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴GK= ![]() .
.
【解析】(1)由AB是直径和MB是⊙O的切线,易证得∠CBF=∠FAB,再根据角平分线的定义和同弧所对的圆周角相等,可证得结论。
(2)根据题意,易证得四边形ODMB是正方形,根据正方形的每一条对角线平分一组对角,得到∠DBO=45°,再由圆周角的性质,可证得∠BAC=∠ACB=45°,即可得出△ABC是等腰直角三角形.
(3)先证明△BAP≌△BCG得出BP=BG,再证明四边形MNBH是平行四边形,得出MN=BH,然后证明△PCM≌△PCB、△ABE≌△BCN得出对应边相等,设BE=CN=a,则BH=MN=2a,易证△PCM≌△PCB,建立方程求出相关线段的长,根据勾股定理及平行得线段成比例,建立方程,求解即可求得GK的值。
【考点精析】关于本题考查的平行四边形的判定与性质和切线的判定定理,需要了解若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平行四边形ABCD中,AE是BC边上的高,将△ABE沿BC方向平移,使点E与点C重合,得△GFC.
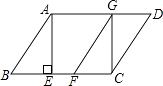
(1)求证:BE=DG;
(2)已知tanB= ,AB=5,若四边形ABFG是菱形,求平行四边形ABCD的面积.
,AB=5,若四边形ABFG是菱形,求平行四边形ABCD的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某文教店用1200元购进了甲、乙两种钢笔.已知甲种钢笔进价为每支12元,乙种钢笔进价为每支l0元.文教店在销售时甲种钢笔售价为每支l5元,乙种钢笔售价为每支l2元,全部售完后共获利270元.
(1)求这个文教店购进甲、乙两种钢笔各多少支?
(2)若该文教店以原进价再次购进甲、乙两种钢笔,且购进甲种钢笔的数量不变,而购进乙种钢笔的数量是第一次的2倍,乙种钢笔按原售价销售,而甲种钢笔降价销售.当两种钢笔销售完毕时,要使再次购进的钢笔获利不少于340元,甲种钢笔最低售价每支应为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】江汉平原享有“中国小龙虾之乡”的美称,甲、乙两家农贸商店,平时以同样的价格出售品质相同的小龙虾,“龙虾节”期间,甲、乙两家商店都让利酬宾,付款金额y甲、y乙(单位:元)与原价x(单位:元)之间的函数关系如图所示:
(1)直接写出y甲,y乙关于x的函数关系式;
(2)“龙虾节”期间,如何选择甲、乙两家商店购买小龙虾更省钱?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=﹣x2+bx+c与x轴交于A,B与y轴交于C,过C作x轴的平行线交抛物线于点D,过点D作x轴的垂线交x轴于E,点D的坐标为(2,3)
(1)求抛物线的解析式;
(2)点P为第一象限直线DE右侧抛物线上一点,连接AP交y轴于点F,连接PD、DF,设点P的横坐标为t,△PFD的面积为S,求S与t的函数关系式;
(3)在(2)的条件下,点P向下平移3个单位得到点Q,连接AQ、EQ,若∠AQE=45°,求点P的横坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】网络商店(简称网店)是近年来迅速兴起的一种电子商务形式,小明的网店销售红枣、小米两种商品的相关信息如下表:
商品
红枣
小米
规格
1kg/袋
2kg/袋
成本(元/袋)
40
38
售价(元/袋)
60
54
根据上表提供的信息,解答下列问题
(1)已知今年前四个月,小明的网店销售上表中规格的红枣和小米共2000kg,获得利润2.8万元,求这前四个月小明的网店销售这种规格的红枣和小米各多少袋?
(2)根据之前的销售情况,估计今年5月到12月这后八个月,小明的网店还能销售同规格的红枣和小米共4000kg,其中,红枣的销售量不低于1200kg.假设这后八个月,销售红枣x(kg),销售红枣和小米获得的总利润为y(元),求出y与x之间的函数关系式,并求出这后八个月,小明的网店销售这种规格的红枣和小米至少获得总利润多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.(ab)2=ab2
B.3a+2a2=5a2
C. =﹣4
=﹣4
D.aa=a2
相关试题

