【题目】我市某工艺厂为配合北京奥运,设计了一款成本为20元∕件的工艺品投放市场进行试销.经过调查,得到如下数据:
销售单价x(元/件) | … | 30 | 40 | 50 | 60 | … |
每天销售量y(件) | … | 500 | 400 | 300 | 200 | … |
(1)把上表中x、y的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想y与x的函数关系,并求出函数关系式;
(2)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?(利润=销售总价﹣成本总价)
(3)当地物价部门规定,该工艺品销售单价最高不能超过45元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?

参考答案:
【答案】(1)![]() 与
与![]() 的函数关系是一次函数的关系,
的函数关系是一次函数的关系,
函数关系式为y=-10x+800 (20<x<80)
(2)设工艺厂试销该工艺品每天获得的利润为L元
则 L=(x-20)(-10x+800)
=-10(x-50)2+9000
∴当销售单价定为50元时,每天获得的利润最大,最大利润是9000元。
(3)由(2)知当x<50时,y随x的增大而增大,
∴当x=45时有最大值,
∴当销售单价定为45元时,每天获得的利润最大
【解析】分析:(1)从表格中的数据我们可以看出当x增加10时,对应y的值减小100,所以y与x之间可能是一次函数的关系,我们可以根据图象发现这些点在一条直线上,所以y与x之间是一次函数的关系,然后设出一次函数关系式,求出其关系式.
(2)利用二次函数的知识求最大值.
解:(1)画图如图;
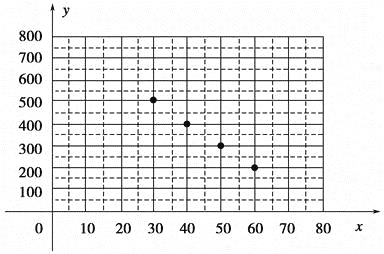
由图可猜想y与x是一次函数关系,
设这个一次函数为y=kx+b(k≠0)
∵这个一次函数的图象经过(30,500)、(40,400)这两点,
∴![]() ,解得
,解得![]()
∴函数关系式是:y=-10x+800.
(2)设工艺厂试销该工艺品每天获得的利润是W元,依题意得
W=(x-20)(-10x+800)
=-10x2+1000x-16000
=-10(x-50)2+9000
∴当x=50时,W有最大值9000.
所以,当销售单价定为50元∕件时,工艺厂试销该工艺品每天获得的利润最大,最大利润是9000元.
(3)对于函数W=-10(x-50)2+9000,
当x≤45时,W的值随着x值的增大而增大,销售单价定为45元∕件时,工艺厂试销该工艺品每天获得的利润最大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】到三角形三边所在直线距离相等的点有__________个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明骑车从家出发,先向东骑行1km到达A村,继续向东骑行4km到达B村,然后向西骑行8km到达C村,最后回到家.
(1)以家为原点,以向东方向为正方向,用1 cm表示1 km,画出数轴,并在数轴上表示出A、B、C三个村的位置;
(2)C村离A村有多远?
(3)小明一共骑行了多少千米? -
科目: 来源: 题型:
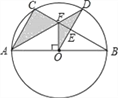
查看答案和解析>>【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,FO⊥AB,垂足为点O,连接AF并延长交⊙O于点D,连接OD交BC于点E,∠B=30°,FO=2
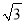 .
.(1)求AC的长度;
(2)求图中阴影部分的面积.(计算结果保留根号)
-
科目: 来源: 题型:
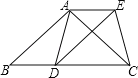
查看答案和解析>>【题目】已知:如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD,EC.
(1)求证:AD=CE;
(2)当点D在什么位置时,四边形ADCE是矩形,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a、b、c是△ABC的三边长,且方程a(1+x2)+2bx﹣c(1﹣x2)=0的两根相等,则△ABC为( )
A. 等腰三角形 B. 直角三角形 C. 等边三角形 D. 任意三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】七年级一班开展了一次“纪念抗日战争胜利七十周年”知识竞赛,竞赛题一共有20道题,下表是其中四位参赛选手的答对题数和不答或答错题数及得分情况,请你根据表格中所给的信息回答下列问题:
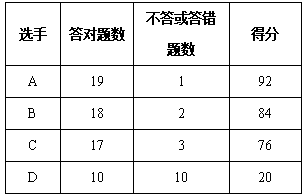
(1)问答对一题得多少分,不答或答错一题扣多少分?
(2)一位同学说他得了75分,请问可能吗?请说明理由.
相关试题

