【题目】如图是用大小相等的小五角星按一定规律拼成的一组图案,第1个图案中有4颗五角星,第2个图案中有7颗五角星,第3个图案中有10颗五角星,…,请根据你的观察完成下列问题.

(1)根据上述规律,分别写出第4个图案和第5个图案中小五角星的颗数;
(2)按如图所示的规律,求出第![]() 个图案中小五角星的颗数(用含
个图案中小五角星的颗数(用含![]() 的代数式表示);
的代数式表示);
(3)求第2019个图案中小五角星的颗数?
参考答案:
【答案】(1)第4个图案中小五角星的颗数为13;第5个图案中小五角星的颗数为16;(2)3n+1;(3)6058.
【解析】
(1)观察图形,将图形中的五角星分成两部分,根据各图形中五角星个数的变化可找出第4个图案和第5个图案中小五角星的颗数;
(2)根据各图形中五角星个数的变化,可得出第n个图案中有(3n+1)颗五角星;
(3)代入n=2019即可求出结论.
解:(1)观察图形,将图形中的五角星分成两部分,根据各图形中五角星个数的变化可找出第4个图案中小五角星的颗数=3×4+1=13;第5个图案中小五角星的颗数=3×5+1=16;
(2)∵第1个图案中有4=3×1+1颗五角星,第2个图案中有7=3×2+1颗五角星,第3个图案中有10=3×3+1颗五角星,第4个图案中有13=3×4+1颗五角星,第5个图案中有16=3×5+1颗五角星,…,
∴第n个图案中有(3n+1)颗五角星;
(3)当n=2019时,3n+1=6058,
∴第2019个图案中有6058颗五角星.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC中,CA=CB,∠ACB=90°,直线l经过点C,AF⊥l于点F,BE⊥l于点E.
(1)求证:△ACF≌△CBE;
(2)将直线旋转到如图2所示位置,点D是AB的中点,连接DE.若AB=
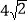 ,∠CBE=30°,求DE的长.
,∠CBE=30°,求DE的长.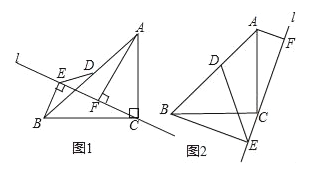
-
科目: 来源: 题型:
查看答案和解析>>【题目】“中华紫薇园”景区今年“五一”期间开始营业,为方便游客在园区内游玩休息,决定向一家园艺公司采购一批户外休闲椅,经了解,公司出售两种型号休闲椅,如下表:
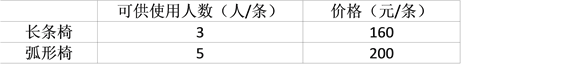
景区采购这批休闲椅共用去56000元,购得的椅子正好可让1300名游客同时使用.
(1)求景区采购了多少条长条椅,多少条弧形椅?
(2)景区现计划租用A、B两种型号的卡车共20辆将这批椅子运回景区,已知A型卡车每辆可同时装运4条长条椅和11条弧形椅,B型卡车每辆可同时装运12条长条椅和7条弧形椅.如何安排A、B两种卡车可一次性将这批休闲椅运回来?
(3)又知A型卡车每辆的运费为1200元,B型卡车每辆的运费为1050元,在(2)的条件下,若要使此次运费最少,应采取哪种方案?并求出最少的运费为多少元.
-
科目: 来源: 题型:
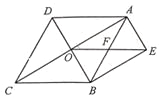
查看答案和解析>>【题目】如图,菱形ABCD的对角线AC、BD相交于点O,BE∥AC,AE∥BD,OE与AB交于点F.
(1)试判断四边形AEBO的形状,并说明理由;
(2)若OE=10,AC=16,求菱形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列两个等式:
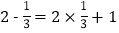 ,
,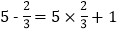 ,给出定义如下:我们称使等式
,给出定义如下:我们称使等式 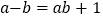 成立的一对有理数
成立的一对有理数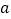 ,
, 为“共生有理数对”,记为(
为“共生有理数对”,记为(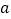 ,
, ),如:数对(
),如:数对(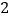 ,
, ),(
),(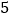 ,
, ),都是“共生有理数对”.
),都是“共生有理数对”.(1)数对(
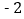 ,
,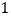 ),(
),(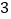 ,
, )中是“共生有理数对”吗?说明理由.
)中是“共生有理数对”吗?说明理由. (2)若(
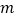 ,
,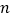 )是“共生有理数对”,则(
)是“共生有理数对”,则(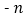 ,
,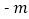 )是“共生有理数对”吗?说明理由.
)是“共生有理数对”吗?说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】永辉超市销售茶壶、茶杯,茶壶每只定价20元,茶杯每只4元.今年“双十一”期间超市将开展促销活动,向顾客提供两种优惠方案:
方案一:每买一只茶壶就赠一只茶杯;
方案二:茶壶和茶杯都按定价的90%付款.
某顾客计划到该超市购买茶壶5只和茶杯
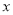 只(茶杯数多于5只).
只(茶杯数多于5只).(1)用含
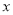 的代数式分别表示方案一与方案二各需付款多少元?
的代数式分别表示方案一与方案二各需付款多少元?(2)当
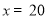 时,请通过计算说明该顾客选择上面的两种购买方案哪种更省钱?
时,请通过计算说明该顾客选择上面的两种购买方案哪种更省钱?(3)当
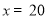 时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法.
时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=4,BC=6,E是BC边的中点,点P在线段AD上,过P作PF⊥AE于F,设PA=x.
(1)求证:△PFA∽△ABE;
(2)当点P在线段AD上运动时,设PA=x,是否存在实数x,使得以点P,F,E为顶点的三角形也与△ABE相似?若存在,请求出x的值;若不存在,请说明理由;
(3)探究:当以D为圆心,DP为半径的⊙D与线段AE只有一个公共点时,请直接写出x满足的条件: .

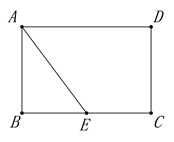
备用图
相关试题

