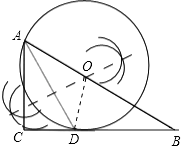
【题目】已知:如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D. 
(1)以AB边上一点O为圆心,过A、D两点作⊙O(不写作法,保留作图痕迹),再判断直线BC与⊙O的位置关系,并说明理由;
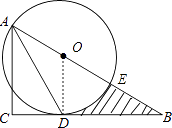
(2)若(1)中的⊙O与AB边的另一个交点为E,AB=6,BD=2 ![]() ,求线段BD、BE与劣弧DE所围成的图形面积.(结果保留根号和π)
,求线段BD、BE与劣弧DE所围成的图形面积.(结果保留根号和π)
参考答案:
【答案】
(1)解:如图:连接OD,
∵OA=OD,
∴∠OAD=∠ADO,
∵∠BAC的角平分线AD交BC边于D,
∴∠CAD=∠OAD,
∴∠CAD=∠ADO,
∴AC∥OD,
∵∠C=90°,
∴∠ODB=90°,
∴OD⊥BC,
即直线BC与⊙O的切线,
∴直线BC与⊙O的位置关系为相切
(2)解:设⊙O的半径为r,则OB=6﹣r,又BD=2 ![]() ,
,
在Rt△OBD中,
OD2+BD2=OB2,
即r2+(2 ![]() )2=(6﹣r)2,
)2=(6﹣r)2,
解得r=2,OB=6﹣r=4,
∴∠DOB=60°,
∴S扇形ODE= ![]() =
= ![]() π,
π,
S△ODB= ![]() ODBD=
ODBD= ![]() ×2×2
×2×2 ![]() =2V,
=2V,
∴线段BD、BE与劣弧DE所围成的图形面积为:S△ODB﹣S扇形ODE=2 ![]() ﹣
﹣ ![]() π.
π.
【解析】(1)根据题意得:O点应该是AD垂直平分线与AB的交点;由∠BAC的角平分线AD交BC边于D,与圆的性质可证得AC∥OD,又由∠C=90°,则问题得证;(2)设⊙O的半径为r.则在Rt△OBD中,利用勾股定理列出关于r的方程,通过解方程即可求得r的值;然后根据扇形面积公式和三角形面积的计算可以求得“线段BD、BE与劣弧DE所围成的图形面积为:S△ODB﹣S扇形ODE=2 ![]() ﹣
﹣ ![]() π”.
π”.
【考点精析】本题主要考查了勾股定理的概念和扇形面积计算公式的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2)才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,锐角△ABC的两条高BD、CE相交于点O,且OB=OC.

(1)求证:△ABC是等腰三角形;
(2)判断点O是否在∠BAC的角平分线上,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】古运河是扬州的母亲河.为打造古运河风光带,现有一段长为180米的河道整治任务由A、B两工程队先后接力完成.A工程队每天整治12米,B工程队每天整治8米,共用时20天.
(1)根据题意,甲、乙两名同学分别列出尚不完整的方程组如下: 甲: ;乙:
;乙: 
根据甲、乙两名问学所列的方程组,请你分别指出未知数x、y表示的意义,然后在方框中补全甲、乙两名同学所列的方程组:
甲:x表示 , y表示;
乙:x表示 , y表示 .
(2)求A、B两工程队分别整治河道多少米.(写出完整的解答过程) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某品牌太阳能热水器的实物图和横断面示意图,已知真空集热管与支架CD所在直线相交于水箱横断面⊙O的圆心O,支架CD与水平面AE垂直,AB=150厘米,∠BAC=30°,另一根辅助支架DE=76厘米,∠CED=60°.
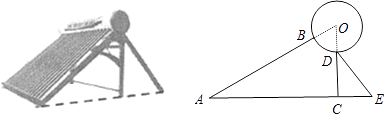
(1)求垂直支架CD的长度;(结果保留根号)
(2)求水箱半径OD的长度.(结果保留三个有效数字,参考数据: ≈1.414,
≈1.414,  ≈1.73)
≈1.73) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是甲、乙两个圆柱形水槽的轴截面示意图,乙槽中有一圆柱形铁块立放其中(圆柱形铁块的下底面完全落在乙槽底面上).现将甲槽中的水匀速注人乙槽,甲、乙两个水槽中水的深度y(厘米)与注水时间x(分钟)之间的关系如图2所示.根据图象提供的信息,解答下列问题:
(1)图2中折线ABC表示槽中水的深度与注水时间之间的关系,线段DE表示槽中水的深度与注水时间之间的关系(以上两空选塡“甲”或“乙”),点B的纵坐标表示的实际意义是;
(2)注水多长时间时,甲、乙两个水槽中水的深度相同;
(3)若乙槽底面积为36平方厘米(壁厚不计),求乙槽中铁块的体积;
(4)若乙槽中铁块的体积为112立方厘米,求甲槽底面积(壁厚不计).(直接写成结果)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2)
(1)写出点A、B的坐标:
A( , )、B( , )
(2)判断△ABC的形状 .计算△ABC的面积是 .
(3)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,A′B′C′的三个顶点坐标分别是A′( , ),B′( , ),C′( , )

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠BAC=90°,AB<AC,M是BC边的中点,MN⊥BC交AC于点N.动点P从点B出发沿射线BA以每秒
 厘米的速度运动.同时,动点Q从点N出发沿射线NC运动,且始终保持MQ丄MP.设运动时间为t秒(t>0).
厘米的速度运动.同时,动点Q从点N出发沿射线NC运动,且始终保持MQ丄MP.设运动时间为t秒(t>0).
(1)△PBM与△QNM相似吗?以图1为例说明理由;
(2)若∠ABC=60°,AB=4 厘米. ①求动点Q的运动速度;
厘米. ①求动点Q的运动速度;
②设△APQ的面积为S(平方厘米),求S与t的函数关系式.
相关试题

