【题目】如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN,求线段CN长. 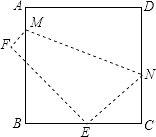
参考答案:
【答案】解:设CN=xcm,则DN=(8﹣x)cm,由折叠的性质知EN=DN=(8﹣x)cm, 而EC= ![]() BC=4cm,在Rt△ECN中,由勾股定理可知EN2=EC2+CN2 ,
BC=4cm,在Rt△ECN中,由勾股定理可知EN2=EC2+CN2 ,
即(8﹣x)2=16+x2 ,
整理得16x=48,
解得:x=3.
即线段CN长为3
【解析】根据折叠的性质,只要求出DN就可以求出NE,在直角△CEN中,若设CN=x,则DN=NE=8﹣x,CE=4cm,根据勾股定理就可以列出方程,从而解出CN的长.
【考点精析】利用翻折变换(折叠问题)对题目进行判断即可得到答案,需要熟知折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,△ABC中,AB=AC,点D、E、F分别为AB、AC、BC边的中点.求证:DE与AF互相垂直平分.
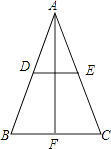
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为原点,在数轴上点A表示的数为a,点B表示的数为b,且a,b满足|a+2|+(3a+b)2=0.

(1)a=________,b=_________;
(2)若点P从点A出发,以每秒1个单位长度的速度沿数轴向右匀速运动,设运动的时间为t(秒).
①当点P运动到线段OB上,且PO=2PB时,求t的值;
②先取OB的中点E,当点P在线段OE上时,再取AP的中点F,试探究
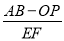 的值是否为定值?若是,求出该值;若不是,请用含t的代数式表示.
的值是否为定值?若是,求出该值;若不是,请用含t的代数式表示.③若点P从点A出发,同时,另一动点Q从点B出发,以每秒2个单位长度的速度向左匀速运动,到达点O后立即原速返回向右匀速运动,当PQ=1时,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校有300名学生参加毕业考试,其数学成绩在100﹣110分之间的有180人,则在100﹣110分之间的频率是( )
A.0.6
B.0.5
C.0.3
D.0.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,点P从点A出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B运动.规定其中一个动点到达端点时,另一个动点也随之停止运动,设运动时间为t(s).
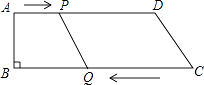
(1)当t为何值时,PQ∥CD?
(2)当t为何值时,PQ=CD? -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将点(﹣2,﹣3)向上平移3个单位,则平移后的点的坐标为________
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的半径为3,直线l与⊙O相交,则圆心O到直线l的距离d的取值范围是( )
A.d=3B.d>3C.0≤d<3D.d<3
相关试题

