【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,点P从点A出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B运动.规定其中一个动点到达端点时,另一个动点也随之停止运动,设运动时间为t(s). 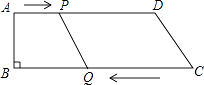
(1)当t为何值时,PQ∥CD?
(2)当t为何值时,PQ=CD?
参考答案:
【答案】
(1)解:根据题意得:PA=t,CQ=3t,则PD=AD﹣PA=24﹣t.
∵AD∥BC,
即PQ∥CD,
∴当PD=CQ时,四边形PQCD为平行四边形,
即24﹣t=3t,
解得:t=6,
即当t=6时,PQ∥CD
(2)解:若PQ=DC,分两种情况:
①PQ=DC,由(1)可知,t=6,
②PQ≠CC,由QC=PD+2(BC﹣AD),
可得方程:3t=24﹣t+4,
解得:t=7
【解析】(1)由当PQ∥CD时,四边形PQCD为平行四边形,可得方程24﹣t=3t,解此方程即可求得答案;(2)根据PQ=CD,一种情况是:四边形PQCD为平行四边形,可得方程24﹣t=3t,一种情况是:四边形PQCD为等腰梯形,可求得当QC﹣PD=QC﹣EF=QF+EC=2CE,即3t﹣(24﹣t)=4时,四边形PQCD为等腰梯形,解此方程即可求得答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为原点,在数轴上点A表示的数为a,点B表示的数为b,且a,b满足|a+2|+(3a+b)2=0.

(1)a=________,b=_________;
(2)若点P从点A出发,以每秒1个单位长度的速度沿数轴向右匀速运动,设运动的时间为t(秒).
①当点P运动到线段OB上,且PO=2PB时,求t的值;
②先取OB的中点E,当点P在线段OE上时,再取AP的中点F,试探究
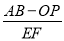 的值是否为定值?若是,求出该值;若不是,请用含t的代数式表示.
的值是否为定值?若是,求出该值;若不是,请用含t的代数式表示.③若点P从点A出发,同时,另一动点Q从点B出发,以每秒2个单位长度的速度向左匀速运动,到达点O后立即原速返回向右匀速运动,当PQ=1时,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校有300名学生参加毕业考试,其数学成绩在100﹣110分之间的有180人,则在100﹣110分之间的频率是( )
A.0.6
B.0.5
C.0.3
D.0.1 -
科目: 来源: 题型:
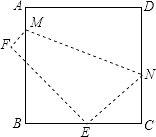
查看答案和解析>>【题目】如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN,求线段CN长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将点(﹣2,﹣3)向上平移3个单位,则平移后的点的坐标为________
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的半径为3,直线l与⊙O相交,则圆心O到直线l的距离d的取值范围是( )
A.d=3B.d>3C.0≤d<3D.d<3
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班准备买一些乒乓球和乒乓球拍,先了解情况如下:甲、乙两家商店出售有同样品牌的乒乓球和乒乓球拍,乒乓球拍每副30元,乒乓球每盒定价5元,经洽谈后,甲店没卖一副球拍赠一盒乒乓球,乙店全部按定价的9折优惠,该班需球拍5副,乒乓球若干盒(不少于5盒).
(1)当购买多少盒乒乓球时,两种优惠办法付款一样?
(2)当购买30盒乒乓球时,去哪家商店购买更划算?
(3)当购买30盒乒乓球时,你有其它的更好的省钱方案吗?并计算费用。
相关试题

