【题目】如图,是一块破损的木板.
(1)请你设计一种方案,检验木板的两条直线边缘 AB、CD 是否平行;
(2)若 AB∥CD,连接 BC,过点 A 作 AM⊥BC 于 M,垂足为 M,画出图形,并写出∠BCD 与∠BAM 的数量关系.

参考答案:
【答案】(1)见解析;(2)∠BCD+∠BAM=90°.
【解析】
(1)根据平行线的判定即可得;
(2)根据题意作图即可得,再利用平行线的性质与直角三角形两锐角互余可得答案.
(1)根据同位角相等,两直线平行,可以画一条直线截线段 AB 与CD,测量一对同位角,如果相等,则 AB∥CD,反之,则不平行.
(2)如图所示:

∵AB∥CD,
∴∠BCD=∠ABC,
∵AM⊥BC,
∴∠ABC+∠BAM=90°, 则∠BCD+∠BAM=90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是用大小相等的小正方形按一定规律拼成的,则第10个图形是_________个小正方形,第n 个图形是___________个小正方形.

-
科目: 来源: 题型:
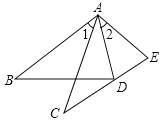
查看答案和解析>>【题目】在数学课上,林老师在黑板上画出如图所示的△ABD和△ACE两个三角形,并写出四个条件:①AB=AC;②AD=AE;③∠1=∠2;④∠B=∠C.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.
题设:___________;结论:_______.(均填写序号)
证明:
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.
(1)从图中任找两组全等三角形;
(2)从(1)中任选一组进行证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费,为更好地做决策,自来水公司随机抽取部分用户的用水量数据,并绘制了如图不完整的统计图(每组数据包括最大值但不包括最小值),请你根据统计图解决下列问题:
(1)此次抽样调查的样本容量是
(2)补全左侧统计图,并求扇形统计图中“25吨~30吨”部分的圆心角度数.
(3)如果自来水公司将基本用水量定为每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格?

-
科目: 来源: 题型:
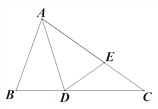
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=2∠C,∠BAC的平分线AD交BC于D,E为AC上一点,AE=AB,连接DE.
(1)求证:△ABD≌△AED;
(2)已知BD=5,AB=9,求AC长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:善于思考的小明在解方程组
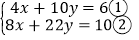 时,采用了一种“整体代换”的解法,解法如下:
时,采用了一种“整体代换”的解法,解法如下:解:将方程②8x+20y+2y=10,变形为 2(4x+10y)+2y=10③,把方程①代入③得,2×6+2y=10,则 y=﹣1;把 y=﹣1 代入①得,x=4,所以方程组的解为:
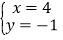 请你解决以下问题:
请你解决以下问题:(1)试用小明的“整体代换”的方法解方程组
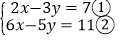
(2)已知 x、y、z,满足
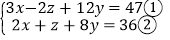 试求 z 的值.
试求 z 的值.
相关试题

