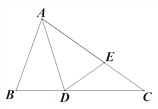
【题目】如图,在△ABC中,∠ABC=2∠C,∠BAC的平分线AD交BC于D,E为AC上一点,AE=AB,连接DE.
(1)求证:△ABD≌△AED;
(2)已知BD=5,AB=9,求AC长.
参考答案:
【答案】(1)证明见解析; (2)AC=14
【解析】
试题(1)由AD是∠BAC的平分线,得出∠BAD=∠DAC,根据已知条件可证△ABD≌△AED;
(2)由△ABD≌△AED 得BD=DE,∠B=∠AED,再利用三角形外角的性质求证CE=DE,然后问题可解.
试题解析:(1)∵∠BAC的平分线AD交BC边于点D,
∴∠BAD=∠DAC,
在△ABD与△AED中,
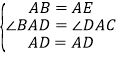 ,
,
∴△ABD≌△AED(SAS);
(2)∵△ABD≌△AED
∴BD=DE,∠B=∠AED,
∵∠B=2∠C,∠AED=∠C+∠EDC,
∴∠AED=2∠C,
∴∠C=∠EDC,
∴CE=DE,
∴CE=BD,
∴AC=AE+EC=AB+BD.
∵BD=5,AB=9
∴AC=14.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.
(1)从图中任找两组全等三角形;
(2)从(1)中任选一组进行证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是一块破损的木板.
(1)请你设计一种方案,检验木板的两条直线边缘 AB、CD 是否平行;
(2)若 AB∥CD,连接 BC,过点 A 作 AM⊥BC 于 M,垂足为 M,画出图形,并写出∠BCD 与∠BAM 的数量关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费,为更好地做决策,自来水公司随机抽取部分用户的用水量数据,并绘制了如图不完整的统计图(每组数据包括最大值但不包括最小值),请你根据统计图解决下列问题:
(1)此次抽样调查的样本容量是
(2)补全左侧统计图,并求扇形统计图中“25吨~30吨”部分的圆心角度数.
(3)如果自来水公司将基本用水量定为每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格?

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:善于思考的小明在解方程组
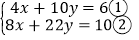 时,采用了一种“整体代换”的解法,解法如下:
时,采用了一种“整体代换”的解法,解法如下:解:将方程②8x+20y+2y=10,变形为 2(4x+10y)+2y=10③,把方程①代入③得,2×6+2y=10,则 y=﹣1;把 y=﹣1 代入①得,x=4,所以方程组的解为:
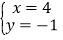 请你解决以下问题:
请你解决以下问题:(1)试用小明的“整体代换”的方法解方程组
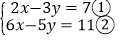
(2)已知 x、y、z,满足
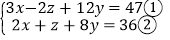 试求 z 的值.
试求 z 的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,∠BAC=90°,AB=AC,MN是经过点A的直线,BD⊥MN,CE⊥MN,垂足分别为D,E.
(1)求证:①∠BAD=∠ACE;②BD=AE.
(2)请写出BD,CE,DE三者间的数量关系式,并证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为奖励在趣味运动会上取得好成绩的员工,计划购买甲、乙两种奖品共20件,其中甲种奖品每件40元,乙种奖品每件30元.
(1)如果购买甲、乙两种奖品共花费了650元,求甲、乙两种奖品各购买了多少件;
(2)如果购买乙种奖品的件数不超过甲种奖品件数的2倍,总花费不超过680元,求该公司有哪几种不同的购买方案.
相关试题

