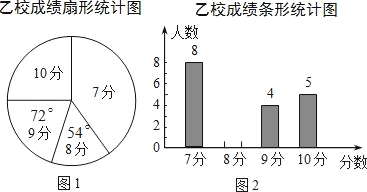
【题目】（10分）甲、乙两校参加市教育局举办的初中生英语口语竞赛，两校参赛人数相等．比赛结束后，发现学生成绩分别为7分、8分、9分、10分（满分为10分）．依据统计数据绘制了如下尚不完整的统计图表．

分数

7分

8分

9分

10分

人数

11

0

　 　

8

（1）请将甲校成绩统计表和图2的统计图补充完整；

（2）经计算，乙校的平均分是8.3分，中位数是8分，请写出甲校的平均分、中位数；并从平均分和中位数的角度分析哪个学校成绩较好．

参考答案：

【答案】（1）见解析；（2）见解析

【解析】试题分析：（1）根据已知10分的有5人，所占扇形圆心角为90°，可以求出总人数，即可得出甲校9分的人数和乙校8分的人数，从而可补全统计图；

（2）根据把分数从小到大排列，利用中位数的定义解答，根据平均数求法得出甲的平均数．

试题解析：（1）根据已知10分的有5人，所占扇形圆心角为90°，可以求出总人数为：

5÷=20（人），

即可得出8分的人数为：20-8-4-5=3（人），

画出图形如图：

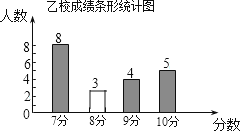
甲校9分的人数是：20-11-8=1（人），

(2)甲校的平均分为=（7×11+8×0+9×1+10×8）=8.3分，

分数从低到高，第10人与第11人的成绩都是7分，

∴中位数=（7+7）=7（分）；

平均分相同，乙的中位数较大，因而乙校的成绩较好．

关闭