【题目】如图，在平面直角坐标系中，抛物线y=﹣x2+bx+c与x轴交于A（﹣3，0）、B（1，0）两点，与y轴交于点C，D是抛物线的顶点，E是对称轴与x轴的交点．

（1）求抛物线的解析式，并在﹣4≤x≤2范围内画出此抛物线的草图；

（2）若点F和点D关于x轴对称，点P是x轴上的一个动点，过点P作PQ∥OF交抛物线于点Q，是否存在以点O、F、P、Q为顶点的平行四边形？若存在，求出点P坐标；若不存在，请说明理由．

参考答案：

【答案】（1）见解析（2）P1（﹣2，0），P2（2，0），P3（﹣2，0）．

【解析】：试题分析：（1）将A（﹣3，0）、B（1，0）两点带入二次函数表达式，即可求得二次函数解析式，以及顶点D的坐标。进而画出在﹣4≤x≤2范围内此抛物线的草图，可运用描点法画。（2）若存在以点O、F、P、Q为顶点的平行四边形，则F、Q纵坐标的绝对值相等。点F 的坐标已知，可分情况讨论，求点Q坐标，从而求得P点坐标。

试题解析：解：（1）根据题意得： ，解得： ，

∴解析式为y=﹣x2﹣2x+3．

当x=﹣=﹣1时，y=4，

∴顶点D的坐标为（﹣1，4），

∴点F的坐标为（﹣1，﹣4）．

此抛物线的草图如图所示

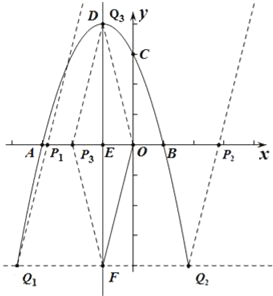
（2）若以O、F、P、Q为顶点的平行四边形存在，

则点Q（x，y）必须满足|y|=|EF|=4．

①当y=﹣4时，﹣x2﹣2x+3=﹣4，

解得，x=﹣1±2，

∴Q1（﹣1﹣2，﹣4），Q2（﹣1+2，﹣4）

∴P1（﹣2，0），P2（2，0）．

②当y=4时，﹣x2﹣2x+3=4，

解得，x=﹣1，

∴Q3（﹣1，4），

∴P3（﹣2，0），

综上所述，符合条件的点有三个即：

P1（﹣2，0），P2（2，0），P3（﹣2，0）．

关闭